[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-17 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1677.628,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T07:17:44.025822+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6552,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5698},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-26T09:04:07","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-17 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.115,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T07:17:44.0261432+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5585,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-17 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.681,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T07:17:44.026293+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5269,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-17 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":387.305,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T07:17:44.0264124+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2442,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-17 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.42,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T07:17:44.0265419+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2721,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-17 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.231,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T07:17:44.0267134+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5711,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-24T14:38:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 201320
05.08.2021, 14:23
0.00 руб.
1
5
0
Здравствуйте, уважаемые эксперты! Прошу помощи в следующей задаче: По ссылке для консультации # 201297 (консультация закрыта) была задача про электрическую цепь с повторяющимися 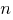 раз сегментами. К сожалению, формула общего сопротивления данной цепи в зависимости от количества ячеек
раз сегментами. К сожалению, формула общего сопротивления данной цепи в зависимости от количества ячеек 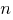 оказалась слишком громоздкой. Возможно, если мы выразим сопротивления
оказалась слишком громоздкой. Возможно, если мы выразим сопротивления 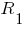 ,
, 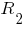 ,
, 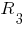 через известное сопротивление
через известное сопротивление 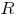 , формулы будут проще. Вот новое условие:
, формулы будут проще. Вот новое условие:
Дана электрическая цепь с повторяющимися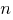 раз сопротивлениями
раз сопротивлениями 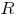 ,
, 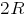 ,
, 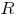 соответственно, которые даны. Выведите точное аналитическое соотношение для эквивалентного сопротивления всей цепи
соответственно, которые даны. Выведите точное аналитическое соотношение для эквивалентного сопротивления всей цепи 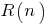 в зависимости от количества ячеек
в зависимости от количества ячеек 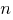 . Сопротивление
. Сопротивление 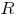 известно.
известно.
Примечание: допустимо при необходимости использовать приложения, упрощающие вычисления (к ним, например, относится MathCad)
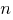 раз сегментами. К сожалению, формула общего сопротивления данной цепи в зависимости от количества ячеек
раз сегментами. К сожалению, формула общего сопротивления данной цепи в зависимости от количества ячеек 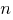 оказалась слишком громоздкой. Возможно, если мы выразим сопротивления
оказалась слишком громоздкой. Возможно, если мы выразим сопротивления 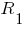 ,
, 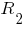 ,
, 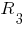 через известное сопротивление
через известное сопротивление 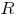 , формулы будут проще. Вот новое условие:
, формулы будут проще. Вот новое условие: Дана электрическая цепь с повторяющимися
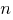 раз сопротивлениями
раз сопротивлениями 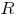 ,
, 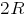 ,
, 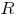 соответственно, которые даны. Выведите точное аналитическое соотношение для эквивалентного сопротивления всей цепи
соответственно, которые даны. Выведите точное аналитическое соотношение для эквивалентного сопротивления всей цепи 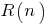 в зависимости от количества ячеек
в зависимости от количества ячеек 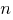 . Сопротивление
. Сопротивление 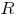 известно.
известно.Примечание: допустимо при необходимости использовать приложения, упрощающие вычисления (к ним, например, относится MathCad)
Прикрепленные файлы:
Обсуждение
07.08.2021, 03:42
общий
Адресаты:
В консультации rfpro.ru/question/201297 я показал Вам формулу "рекуррентное соотношение R(n) в зависимости от R(n-1) , где R(n) - сопротивление цепи с n ячейками". Эта формула позволяет получить искомое Вами "точное аналитическое соотношение для эквивалентного сопротивления всей цепи R(n) в зависимости от количества ячеек n" по-шагово : Сначала для n=1 , затем для n=2 и тд для любого n . Но Вам показалось этого недостаточно.
Перейти от RR-цепочки R1 , R2 , R3 к более простой R , 2·R , R не составит труда Вам, как эксперту. Тогда что Вы хотите?
Верно ли я понимаю Вашу фразу "Выведите точное аналитическое соотношение" как желание получить выражение эквивалентного сопротивления всей цепи R(n) без рекурсии (без использования в формуле предыдущих выражений R(n-1)) ?
Надеюсь, Вы уже поняли, что громоздкость формулы нарастает с увеличением n - к-ва звеньев RR-цепи.
Укажите конкретное максимальное n-значение , при котором Вы будете удовлетворены Решением.
Перейти от RR-цепочки R1 , R2 , R3 к более простой R , 2·R , R не составит труда Вам, как эксперту. Тогда что Вы хотите?
Верно ли я понимаю Вашу фразу "Выведите точное аналитическое соотношение" как желание получить выражение эквивалентного сопротивления всей цепи R(n) без рекурсии (без использования в формуле предыдущих выражений R(n-1)) ?
Надеюсь, Вы уже поняли, что громоздкость формулы нарастает с увеличением n - к-ва звеньев RR-цепи.
Укажите конкретное максимальное n-значение , при котором Вы будете удовлетворены Решением.
07.08.2021, 13:44
общий
Адресаты:
Уважаемый эксперт Владимир Николаевич, мне кажется, что нарастающая громоздкость в формулах зависимости 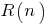 возникала из-за того, что мы не могли выразить соотношения
возникала из-за того, что мы не могли выразить соотношения 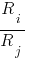 и
и  ;
; 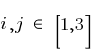 ,
, 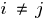 через более простые формулы с меньшим количеством переменных. В условиях данной консультации теперь данные соотношения выражаются через более простые формулы с одной переменной
через более простые формулы с меньшим количеством переменных. В условиях данной консультации теперь данные соотношения выражаются через более простые формулы с одной переменной 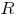 и числовыми коэффициентами. Я уже знаю рекуррентное соотношение
и числовыми коэффициентами. Я уже знаю рекуррентное соотношение 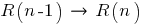 через сопротивления
через сопротивления 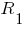 ,
, 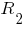 ,
, 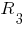 и прекрасно понимаю, что нужно просто подставить
и прекрасно понимаю, что нужно просто подставить 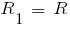 ,
, 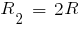 ,
, 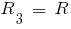 . Вы совершенно правильно поняли, что нужно получить формулу
. Вы совершенно правильно поняли, что нужно получить формулу 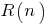 без рекурсии (это я пытался сообщить фразами "
без рекурсии (это я пытался сообщить фразами "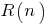 в зависимости от количества ячеек
в зависимости от количества ячеек 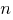 " - не от
" - не от 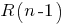 ; "аналитическое соотношение" - не рекуррентное). Как мне кажется, не обязательно знать последовательно значения
; "аналитическое соотношение" - не рекуррентное). Как мне кажется, не обязательно знать последовательно значения 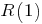 ,
, 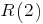 ,
, 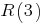 (хотя это требовалось для другого вопроса той консультации), чтобы получить общую зависимость
(хотя это требовалось для другого вопроса той консультации), чтобы получить общую зависимость 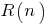 . Мне нужно знать значения
. Мне нужно знать значения 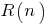 для двух значений
для двух значений 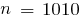 и
и 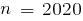 . Надеюсь, ответил на Ваши вопросы.
. Надеюсь, ответил на Ваши вопросы.
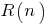 возникала из-за того, что мы не могли выразить соотношения
возникала из-за того, что мы не могли выразить соотношения 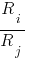 и
и  ;
; 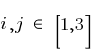 ,
, 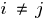 через более простые формулы с меньшим количеством переменных. В условиях данной консультации теперь данные соотношения выражаются через более простые формулы с одной переменной
через более простые формулы с меньшим количеством переменных. В условиях данной консультации теперь данные соотношения выражаются через более простые формулы с одной переменной 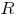 и числовыми коэффициентами. Я уже знаю рекуррентное соотношение
и числовыми коэффициентами. Я уже знаю рекуррентное соотношение 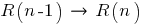 через сопротивления
через сопротивления 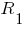 ,
, 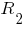 ,
, 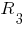 и прекрасно понимаю, что нужно просто подставить
и прекрасно понимаю, что нужно просто подставить 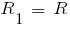 ,
, 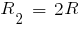 ,
, 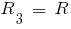 . Вы совершенно правильно поняли, что нужно получить формулу
. Вы совершенно правильно поняли, что нужно получить формулу 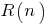 без рекурсии (это я пытался сообщить фразами "
без рекурсии (это я пытался сообщить фразами "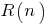 в зависимости от количества ячеек
в зависимости от количества ячеек 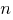 " - не от
" - не от 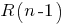 ; "аналитическое соотношение" - не рекуррентное). Как мне кажется, не обязательно знать последовательно значения
; "аналитическое соотношение" - не рекуррентное). Как мне кажется, не обязательно знать последовательно значения 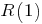 ,
, 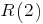 ,
, 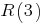 (хотя это требовалось для другого вопроса той консультации), чтобы получить общую зависимость
(хотя это требовалось для другого вопроса той консультации), чтобы получить общую зависимость 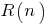 . Мне нужно знать значения
. Мне нужно знать значения 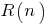 для двух значений
для двух значений 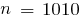 и
и 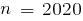 . Надеюсь, ответил на Ваши вопросы.
. Надеюсь, ответил на Ваши вопросы.
07.08.2021, 18:00
общий
Адресаты:
Вы писали: "нарастающая громоздкость в формулах зависимости R(n) возникала из-за того, что мы не могли выразить соотношения Ri / Rj" - мы могли выразить соотношения, и я показал Вам менее громоздкие формулы с мЕньшим числом переменных в нижней строке формул Маткад-скриншота консультации rfpro.ru/question/201297 .
"нужно получить формулу R(n) без рекурсии" - показываю Вам формулы без рекурсии для первых 14 звеньев цепи. Маткад-скриншот прилагаю. Я могу показать больше формул, но программа сервера портит отображение картинок размером сверх лимита 800*800 пикселов (размер сохранённой копии увеличивается, а качество ухудшается). Если Вам удастся уговорить глав-админа сервера (он же Руководитель) увеличить лимит до 1000 пикс), то эксперты смогут верстать более полные и качественные ответы (мои просьбы увеличить лимит проигнорированы).

Когда Вы проанализируете результы вычислений, то поймёте, что с точки зрения физики задача решена ещё в прошлой Вашей консультации q201297. Здесь - те же последовательные и параллельные соединения резисторов, ничего нового. Мы имеем точное значение R0 цепи бесконечной длины. Сопротивление 3х-звенной цепи равно R0 с точностью 1% - что более чем достаточно для практического применения. Увеличение кол-ва звеньев выше 3х экономически неоправдано для техники/электроники. За 45 лет практики я не видел RC или RR-фильтров с кол-вом звеньев более 3х.
Проблемв Вашей задачи - математическая. R0 = ([$8730$]5 + 1)*R выражается иррациональным числом. Значит, оно в принципе не может быть выражено точно. Но требуемое в Условии "точное аналитическое соотношение для эквивалентного сопротивления всей цепи R(n)" можно получить. Для 16-звенной цепи оно равно
R16 = 7049156*R / 2178309 .
Для запрошенных Вами "n = 1010 и n = 2020" выражение будет иметь тот же вид, но вместо 7-значных чисел будут числа в 63 раза длиннее (1010 / 16), то есть 440 цифр. На моём экране с разрешением 1024*768 пикс умещается т-ко 125 цифр в строке.
В Вашей прошлой консультации я советовал Вам "Вы можете создать эту консультацию повторно в разделе Математика со ссылкой на мой недоделанный Ответ в надежде на то, что какой-нибудь математик сформирует "точное аналитическое соотношение R(n)" из моих нарастающе-громоздких маткад-формул". Но Вы снова отправили свой Вопрос в раздел Физика, и я не берусь убивать уйму времени на практически бесполезный синтез длиннючей мат-формулы, чтоб повысить высочайшую точность с 10-13 (для 16-звенной цепи) до абсолютной точности с числами шириной в 4 экрана.
Какой-то легкомысленный преподаватель придумывает для Вас непрактично-издевательские задачки.
"нужно получить формулу R(n) без рекурсии" - показываю Вам формулы без рекурсии для первых 14 звеньев цепи. Маткад-скриншот прилагаю. Я могу показать больше формул, но программа сервера портит отображение картинок размером сверх лимита 800*800 пикселов (размер сохранённой копии увеличивается, а качество ухудшается). Если Вам удастся уговорить глав-админа сервера (он же Руководитель) увеличить лимит до 1000 пикс), то эксперты смогут верстать более полные и качественные ответы (мои просьбы увеличить лимит проигнорированы).

Когда Вы проанализируете результы вычислений, то поймёте, что с точки зрения физики задача решена ещё в прошлой Вашей консультации q201297. Здесь - те же последовательные и параллельные соединения резисторов, ничего нового. Мы имеем точное значение R0 цепи бесконечной длины. Сопротивление 3х-звенной цепи равно R0 с точностью 1% - что более чем достаточно для практического применения. Увеличение кол-ва звеньев выше 3х экономически неоправдано для техники/электроники. За 45 лет практики я не видел RC или RR-фильтров с кол-вом звеньев более 3х.
Проблемв Вашей задачи - математическая. R0 = ([$8730$]5 + 1)*R выражается иррациональным числом. Значит, оно в принципе не может быть выражено точно. Но требуемое в Условии "точное аналитическое соотношение для эквивалентного сопротивления всей цепи R(n)" можно получить. Для 16-звенной цепи оно равно
R16 = 7049156*R / 2178309 .
Для запрошенных Вами "n = 1010 и n = 2020" выражение будет иметь тот же вид, но вместо 7-значных чисел будут числа в 63 раза длиннее (1010 / 16), то есть 440 цифр. На моём экране с разрешением 1024*768 пикс умещается т-ко 125 цифр в строке.
В Вашей прошлой консультации я советовал Вам "Вы можете создать эту консультацию повторно в разделе Математика со ссылкой на мой недоделанный Ответ в надежде на то, что какой-нибудь математик сформирует "точное аналитическое соотношение R(n)" из моих нарастающе-громоздких маткад-формул". Но Вы снова отправили свой Вопрос в раздел Физика, и я не берусь убивать уйму времени на практически бесполезный синтез длиннючей мат-формулы, чтоб повысить высочайшую точность с 10-13 (для 16-звенной цепи) до абсолютной точности с числами шириной в 4 экрана.
Какой-то легкомысленный преподаватель придумывает для Вас непрактично-издевательские задачки.

07.08.2021, 23:15
общий
Адресаты:
Уважаемый эксперт Владимир Николаевич, спасибо большое за Ваш подробный ответ! Преподаватель действительно любит задачи с непростой математикой  !
!
 !
!
09.08.2021, 16:20
общий
Сегодня утром я как обычно вспомнил вчерашний день, Вашу задачу, в мыслях блеснул новый метод её решения, и я снова целый день убил на мелкую продвижку с незаконченным финалом - вот прицепилась зараза!
Мы оба знаем, что в классической математике традиционно принято показывать результат в виде точных, простых дробей типа 1/3 , но не в округлённых значениях 0,333, принятых в физике. Ваше Условие "Выведите точное аналитическое соотношение" означает принудительное использование математического (не физического) стиля. Значит, ищем результат (эквивалентное сопротивления всей цепи R(n)) в виде
Rn(n) = [A(n) / B(n)]*2*R , где R - известное сопротивление, а A(n) и B(n) - натуральные числа (целые и > 0).
Сегодня мне удалось уловить зависимость получения чисто-мат-выражений для числителя A(n) и знаменателя B(n) с помощью Маткада и осмысливания закономерностей его результатов. Но полностью избавиться от рекурсии мне не удалось, не хватает опыта оптимизации функциональных рядов. А Маткад "заточен" для числовой обработки (он не для формул-оптимизации в отличие от MatLab). Да и числовая мощность у Маткада всего 15 знаков точности, что вполне достаточно для технических расчётов, но не для Ваших супер-длинных чисел с запрещённым округлением.

Показываю Вам очередной Маткад-скриншот. Теперь Вы можете создать новую консультацию в разделе Математика, где опытный математик возможно осмелится выразить рекурсию в компактном виде ч-з какие-нибудь факториалы или сумму сходящегося функционального ряда. Только я не могу представить, как он сможет показать Вам ответ с неокругляемыми числами длиной в несколько экранных строк? Ваш преподаватель - большой шутник!
Мы оба знаем, что в классической математике традиционно принято показывать результат в виде точных, простых дробей типа 1/3 , но не в округлённых значениях 0,333, принятых в физике. Ваше Условие "Выведите точное аналитическое соотношение" означает принудительное использование математического (не физического) стиля. Значит, ищем результат (эквивалентное сопротивления всей цепи R(n)) в виде
Rn(n) = [A(n) / B(n)]*2*R , где R - известное сопротивление, а A(n) и B(n) - натуральные числа (целые и > 0).
Сегодня мне удалось уловить зависимость получения чисто-мат-выражений для числителя A(n) и знаменателя B(n) с помощью Маткада и осмысливания закономерностей его результатов. Но полностью избавиться от рекурсии мне не удалось, не хватает опыта оптимизации функциональных рядов. А Маткад "заточен" для числовой обработки (он не для формул-оптимизации в отличие от MatLab). Да и числовая мощность у Маткада всего 15 знаков точности, что вполне достаточно для технических расчётов, но не для Ваших супер-длинных чисел с запрещённым округлением.

Показываю Вам очередной Маткад-скриншот. Теперь Вы можете создать новую консультацию в разделе Математика, где опытный математик возможно осмелится выразить рекурсию в компактном виде ч-з какие-нибудь факториалы или сумму сходящегося функционального ряда. Только я не могу представить, как он сможет показать Вам ответ с неокругляемыми числами длиной в несколько экранных строк? Ваш преподаватель - большой шутник!
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.

