[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1677.372,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T20:30:26.5666882+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6553,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5698},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-26T09:04:07","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.033,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T20:30:26.5668817+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5585,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.603,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T20:30:26.5669653+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5270,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":387.147,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T20:30:26.5670288+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2443,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.338,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T20:30:26.5670993+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2721,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.196,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T20:30:26.5671872+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5712,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-24T14:38:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 202262
08.03.2022, 16:53
0.00 руб.
0
5
2
Здравствуйте! У меня возникли сложности с таким вопросом:
Дано комплексное число a. Требуется:
1)записать числа a и (-a) в алгебраической, тригонометрической и показательной форме;
2)найти все корни уравнения z^3+a=0 и изобразить их на комплексной плоскости.
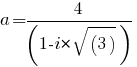
Дано комплексное число a. Требуется:
1)записать числа a и (-a) в алгебраической, тригонометрической и показательной форме;
2)найти все корни уравнения z^3+a=0 и изобразить их на комплексной плоскости.
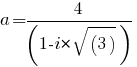
Обсуждение
09.03.2022, 03:24
общий
Адресаты:
Сначала надо избавиться от комплекса в знаменателе, и умножить числитель и знаменатель на сопряжённое число 1 + i·[$8730$]3 .
Получим число "a" в алгебраической форме : a = 1 + i·[$8730$]3
Модуль этого числа M = [$8730$](12 + ([$8730$]3)2) = [$8730$](1+3) = 2 , Мнимая часть im = [$8730$]3 .
Угол [$966$] = arcsin(im / M) = arcsin([$8730$]3 / 2) = [$960$] / 3 рад = 60° .
Число "a" в тригонометрической форме : M·[cos([$966$]) + i·sin([$966$])] = 2·[cos([$960$]/3) + i·sin([$960$]/3)]
Число "a" в показательной форме : M·ei·[$966$] = 2·ei·[$960$]/3
Ваше Уравнение имеет 3 корня: z1 = 0,219 + i·1,241[$8195$] ,[$8195$] z2 = 0,965 - i·0,81[$8195$] ,[$8195$] z3 = -1,184 - i·0,431 .
Дальше сами справитесь?
Получим число "a" в алгебраической форме : a = 1 + i·[$8730$]3
Модуль этого числа M = [$8730$](12 + ([$8730$]3)2) = [$8730$](1+3) = 2 , Мнимая часть im = [$8730$]3 .
Угол [$966$] = arcsin(im / M) = arcsin([$8730$]3 / 2) = [$960$] / 3 рад = 60° .
Число "a" в тригонометрической форме : M·[cos([$966$]) + i·sin([$966$])] = 2·[cos([$960$]/3) + i·sin([$960$]/3)]
Число "a" в показательной форме : M·ei·[$966$] = 2·ei·[$960$]/3
Ваше Уравнение имеет 3 корня: z1 = 0,219 + i·1,241[$8195$] ,[$8195$] z2 = 0,965 - i·0,81[$8195$] ,[$8195$] z3 = -1,184 - i·0,431 .
Дальше сами справитесь?
09.03.2022, 06:59
общий
Адресаты:
Здравствуйте, если можно, покажите решение дальше, а то нам плохо эту тему объяснили, а разобраться и понять хочется. Мне решение не к спеху, так что буду признательна.
09.03.2022, 07:15
общий
Адресаты:
Здравствуйте, Ника! Я ответил на Ваше приветствие, но на Портале принято не засорять посты приветствиями.
На Ваше "покажите решение дальше" мне придётся сверстать подробный Ответ с графиком. Сейчас мне нЕкогда, я планирую сделать это ч-з ~ 12 часов, если другие эксперты не отправят Вам Ответ раньше.
На Портале 4 участника имеют ник "Ника", 2 из них ленятся поблагодарить за помощь, и я вписал их в ЧёрныйСписок, чтоб игнорировать их Вопросы в будущем. Будет хорошо, если Вы заполните свою Регистрационную карту и измените свой ник на уникальный во избежание путаницы.
На Ваше "покажите решение дальше" мне придётся сверстать подробный Ответ с графиком. Сейчас мне нЕкогда, я планирую сделать это ч-з ~ 12 часов, если другие эксперты не отправят Вам Ответ раньше.
На Портале 4 участника имеют ник "Ника", 2 из них ленятся поблагодарить за помощь, и я вписал их в ЧёрныйСписок, чтоб игнорировать их Вопросы в будущем. Будет хорошо, если Вы заполните свою Регистрационную карту и измените свой ник на уникальный во избежание путаницы.
09.03.2022, 17:03
общий
09.03.2022, 17:06
это ответ
Условие: Дано комплексное число a = 4 / (1 - i·[$8730$]3).
Требуется записать числа a и (-a) в алгебраической, тригонометрической и показательной форме;
Вычислить все корни уравнения z3 + a = 0 и изобразить их на комплексной плоскости.
Решение: Вы писали "нам плохо эту тему объяснили", я тоже давно забыл школьную математику. Поэтому читаем вместе замечательную учебную статью "Комплексные числа для чайников" Ссылка1.
В примере5 статьи подробно описано решение Вашего первого пункта. Умножаем знаменатель и числитель на сопряжённое знаменателю выражение (1 + i·[$8730$]3) .
Вспоминаем простую школьную формулу (a - b)·(a + b) = a2 - b2 а также свойство i2 = -1 :
a = 4 / (1 - i·[$8730$]3) = [4·(1 + i·[$8730$]3)] / [(1 - i·[$8730$]3)·(1 + i·[$8730$]3)] = [4·(1 + i·[$8730$]3)] / [12 - (i·[$8730$]3)2] = 4·(1 + i·[$8730$]3)] / [1 - i2·3] = 4·(1 + i·[$8730$]3)] / (1 + 3) = 1 + i·[$8730$]3 - мы получили число "a" в простейшей алгебраической форме.
Модуль этого числа M = [$8730$][12 + ([$8730$]3)2] = [$8730$](1+3) = 2 , Мнимая часть im = [$8730$]3 , действительная часть Re = 1 .
Аргумент комплекса - это угол [$966$] = arctg(im / Re) = arctg([$8730$]3 / 1) = [$960$] / 3 рад = 60° .
Число "a" в тригонометрической форме : M·[cos([$966$]) + i·sin([$966$])] = 2·[cos([$960$]/3) + i·sin([$960$]/3)]
Число "a" в показательной форме : M·ei·[$966$] = 2·ei·[$960$]/3
Для числа -a , обозначим его A = -a , всё аналогично: алгебраическая форма A = -a = -(1 + i·[$8730$]3) = -1 - i·[$8730$]3 ,
Мнимая часть im = -[$8730$]3 , действительная часть Re = -1 .
Модуль этого числа M = [$8730$][(-1)2 + (-[$8730$]3)2] = [$8730$](1+3) = 2 ,
Число A находится в 3й координатной четверти, и его аргумент нужно вычислять по формуле с поправкой:
[$966$] = arctg(im / Re) - [$960$] = arctg[(-[$8730$]3) / (-1)] - [$960$] = arctg([$8730$]3) - [$960$] = [$960$] / 3 - [$960$] = -2·[$960$]/3 рад = -120° .
Число "A" в тригонометрической форме : M·[cos([$966$]) + i·sin([$966$])] = 2·[cos(-2·[$960$]/3) + i·sin(-2·[$960$]/3)]
Число "A" в показательной форме : M·ei·[$966$] = 2·ei·(-2·[$960$]/3)
Вычислим все корни уравнения z3 + a = 0 - перемещаем "a" в правую часть уравнения:
z3 = -a = -1 - i·[$8730$]3 . Этот случай также описан в выше-указанной статье в абзаце "Как извлечь Корень из произвольного комплексного числа?" . Аннотирую:
Уравнение вида zn = w имеет ровно n корней : z0 ; z1 ; z2 ; … кот-е можно найти по формуле:
zk = n[$8730$](M)·{cos[[$966$] + 2·[$960$]·k) / n] + i·sin[[$966$] + 2·[$960$]·k) / n]} , где M = |w| - это модуль комплексного числа w , [$966$] - его аргумент, а параметр k принимает значения : k = {0 ; 1 ; 2 ; … ; n-1} .
В нашем случае n = 3 означает наличие 3х корней уравнения.
-a = -1 - i·[$8730$]3 равно числу "A", для кот-го выше уже вычислены значения M = 2 и [$966$] = -2·[$960$]/3 рад .
Все 3 корня имеют одинаковый модуль Zm = 3[$8730$](M) = 3[$8730$](2) [$8776$] 1,26
Тогда искомые корни:
z0 = Zm·[cos[[$966$] + 2·[$960$]·0) / 3] + i·sin[[$966$] + 2·[$960$]·0) / 3]} = 1,26·[cos(-2·[$960$] / 9) + i·sin(-2·[$960$] / 9)] [$8776$] 0,965 - i·0,81
z1 = Zm·[cos[[$966$] + 2·[$960$]·1) / 3] + i·sin[[$966$] + 2·[$960$]·1) / 3]} = 1,26·[cos(4·[$960$] / 9) + i·sin(4·[$960$] / 9)] [$8776$] 0,219 + i·1,241
z2 = Zm·[cos[[$966$] + 2·[$960$]·2) / 3] + i·sin[[$966$] + 2·[$960$]·2) / 3]} = 1,26·[cos(10·[$960$] / 9) + i·sin(10·[$960$] / 9)] [$8776$] -1,184 - i·0,431
Изображение корней на Комплексной плоскости я выполнил в популярном приложении Маткад (ссылка2) . Маткад избавляет меня от ошибок. Маткад-скриншот с чертежом прилагаю . Я добавил в скрин подробные комментарии зелёным цветом.
 Надеюсь, теперь Вам будет всё понятно. =Удачи!
Надеюсь, теперь Вам будет всё понятно. =Удачи!
Требуется записать числа a и (-a) в алгебраической, тригонометрической и показательной форме;
Вычислить все корни уравнения z3 + a = 0 и изобразить их на комплексной плоскости.
Решение: Вы писали "нам плохо эту тему объяснили", я тоже давно забыл школьную математику. Поэтому читаем вместе замечательную учебную статью "Комплексные числа для чайников" Ссылка1.
В примере5 статьи подробно описано решение Вашего первого пункта. Умножаем знаменатель и числитель на сопряжённое знаменателю выражение (1 + i·[$8730$]3) .
Вспоминаем простую школьную формулу (a - b)·(a + b) = a2 - b2 а также свойство i2 = -1 :
a = 4 / (1 - i·[$8730$]3) = [4·(1 + i·[$8730$]3)] / [(1 - i·[$8730$]3)·(1 + i·[$8730$]3)] = [4·(1 + i·[$8730$]3)] / [12 - (i·[$8730$]3)2] = 4·(1 + i·[$8730$]3)] / [1 - i2·3] = 4·(1 + i·[$8730$]3)] / (1 + 3) = 1 + i·[$8730$]3 - мы получили число "a" в простейшей алгебраической форме.
Модуль этого числа M = [$8730$][12 + ([$8730$]3)2] = [$8730$](1+3) = 2 , Мнимая часть im = [$8730$]3 , действительная часть Re = 1 .
Аргумент комплекса - это угол [$966$] = arctg(im / Re) = arctg([$8730$]3 / 1) = [$960$] / 3 рад = 60° .
Число "a" в тригонометрической форме : M·[cos([$966$]) + i·sin([$966$])] = 2·[cos([$960$]/3) + i·sin([$960$]/3)]
Число "a" в показательной форме : M·ei·[$966$] = 2·ei·[$960$]/3
Для числа -a , обозначим его A = -a , всё аналогично: алгебраическая форма A = -a = -(1 + i·[$8730$]3) = -1 - i·[$8730$]3 ,
Мнимая часть im = -[$8730$]3 , действительная часть Re = -1 .
Модуль этого числа M = [$8730$][(-1)2 + (-[$8730$]3)2] = [$8730$](1+3) = 2 ,
Число A находится в 3й координатной четверти, и его аргумент нужно вычислять по формуле с поправкой:
[$966$] = arctg(im / Re) - [$960$] = arctg[(-[$8730$]3) / (-1)] - [$960$] = arctg([$8730$]3) - [$960$] = [$960$] / 3 - [$960$] = -2·[$960$]/3 рад = -120° .
Число "A" в тригонометрической форме : M·[cos([$966$]) + i·sin([$966$])] = 2·[cos(-2·[$960$]/3) + i·sin(-2·[$960$]/3)]
Число "A" в показательной форме : M·ei·[$966$] = 2·ei·(-2·[$960$]/3)
Вычислим все корни уравнения z3 + a = 0 - перемещаем "a" в правую часть уравнения:
z3 = -a = -1 - i·[$8730$]3 . Этот случай также описан в выше-указанной статье в абзаце "Как извлечь Корень из произвольного комплексного числа?" . Аннотирую:
Уравнение вида zn = w имеет ровно n корней : z0 ; z1 ; z2 ; … кот-е можно найти по формуле:
zk = n[$8730$](M)·{cos[[$966$] + 2·[$960$]·k) / n] + i·sin[[$966$] + 2·[$960$]·k) / n]} , где M = |w| - это модуль комплексного числа w , [$966$] - его аргумент, а параметр k принимает значения : k = {0 ; 1 ; 2 ; … ; n-1} .
В нашем случае n = 3 означает наличие 3х корней уравнения.
-a = -1 - i·[$8730$]3 равно числу "A", для кот-го выше уже вычислены значения M = 2 и [$966$] = -2·[$960$]/3 рад .
Все 3 корня имеют одинаковый модуль Zm = 3[$8730$](M) = 3[$8730$](2) [$8776$] 1,26
Тогда искомые корни:
z0 = Zm·[cos[[$966$] + 2·[$960$]·0) / 3] + i·sin[[$966$] + 2·[$960$]·0) / 3]} = 1,26·[cos(-2·[$960$] / 9) + i·sin(-2·[$960$] / 9)] [$8776$] 0,965 - i·0,81
z1 = Zm·[cos[[$966$] + 2·[$960$]·1) / 3] + i·sin[[$966$] + 2·[$960$]·1) / 3]} = 1,26·[cos(4·[$960$] / 9) + i·sin(4·[$960$] / 9)] [$8776$] 0,219 + i·1,241
z2 = Zm·[cos[[$966$] + 2·[$960$]·2) / 3] + i·sin[[$966$] + 2·[$960$]·2) / 3]} = 1,26·[cos(10·[$960$] / 9) + i·sin(10·[$960$] / 9)] [$8776$] -1,184 - i·0,431
Изображение корней на Комплексной плоскости я выполнил в популярном приложении Маткад (ссылка2) . Маткад избавляет меня от ошибок. Маткад-скриншот с чертежом прилагаю . Я добавил в скрин подробные комментарии зелёным цветом.
5
Спасибо большое, теперь все поняла.
09.03.2022, 18:46
общий
09.03.2022, 19:02
это ответ
1.
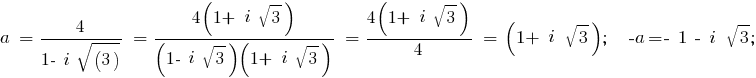
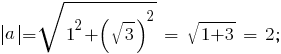
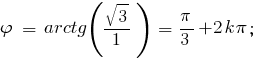
Формула Эйлера (связывает комплексную экспоненту с тригонометрическими функциями)
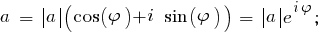
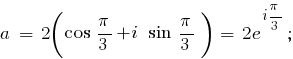
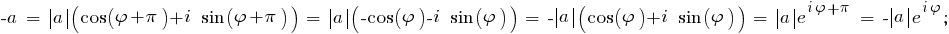
2.
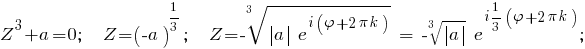
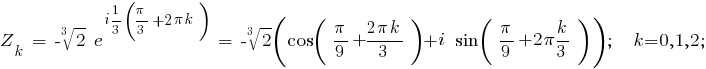
Очевидно, что для k=3,4,5 ... вследствие периодичности функций Cos и Sin можно исключить период 2п, и, следовательно,
уравнение имеет 3 корня.
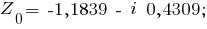
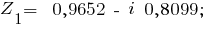
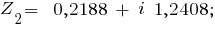

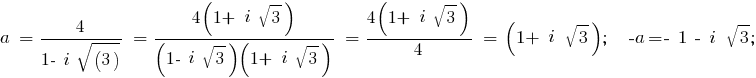
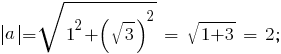
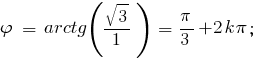
Формула Эйлера (связывает комплексную экспоненту с тригонометрическими функциями)
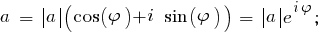
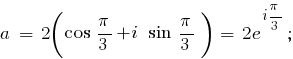
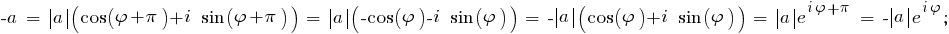
2.
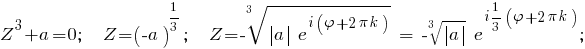
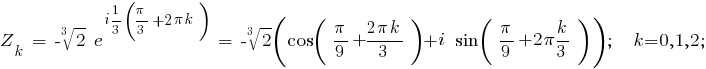
Очевидно, что для k=3,4,5 ... вследствие периодичности функций Cos и Sin можно исключить период 2п, и, следовательно,
уравнение имеет 3 корня.
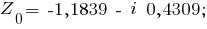
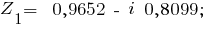
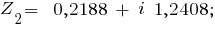
5
Спасибо большое.
Об авторе:
Понеже не словес красных бог слушает, но дел наших хощет
Понеже не словес красных бог слушает, но дел наших хощет
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.

