[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1677.372,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-27T04:58:14.9084888+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6553,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5698},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-26T09:04:07","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.033,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-27T04:58:14.9086462+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5586,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.603,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-27T04:58:14.9087531+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5270,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":387.147,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-27T04:58:14.9088527+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2443,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.338,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-27T04:58:14.9089248+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2722,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.196,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-27T04:58:14.909025+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5712,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-24T14:38:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 202035
06.01.2022, 19:02
0.00 руб.
1
10
0
Здравствуйте, уважаемые эксперты! Прошу вас ответить на следующий вопрос:
В схеме, изображенной на рисунке, после замыкания ключа К через некоторое время т установится стационарный режим. Какая мощность будет выделяться в резисторе R, если начать изменять расстояние между пластинами конденсатора по закону d(t) = d0( 1 + A sin?t), А < 1? Рассмотреть случай быстрых изменений емкости, т.е. когда 2?/? << ?. Заданными параметрами считать ?, A, R. Внутренним сопротивлением батареи пренебречь.

В схеме, изображенной на рисунке, после замыкания ключа К через некоторое время т установится стационарный режим. Какая мощность будет выделяться в резисторе R, если начать изменять расстояние между пластинами конденсатора по закону d(t) = d0( 1 + A sin?t), А < 1? Рассмотреть случай быстрых изменений емкости, т.е. когда 2?/? << ?. Заданными параметрами считать ?, A, R. Внутренним сопротивлением батареи пренебречь.
Прикрепленные файлы:
Обсуждение
07.01.2022, 13:53
общий
Адресаты:
Признаки хороших (качественных) задач - наличие всех необходимых данных для Решения, отсутствие мусора, и хоть какая-нибудь практическая польза от решения (чтоб навык решения пригодился позже в жизни).
В Вашей задаче ключ К - это мусор. Его можно сразу выбросить заменой ключа на эл-схеме перемычкой. Потому что согласно Условию этот ключ замкнули и поехали дальше (искать приключений).
А дальше изменение расстояния м-ду пластинами конденсатора изменяет его ёмкость C = q / U .
При неизменном U = E от изменения C мы получаем изменение зарядов q(t) = U*C(t) = E*C(t) .
А перетекание зарядов по контуру цепи - есть переменный ток, который греет (теоретически) резистор R , на котором и выделяется искомая тепловая мощность.
Однако, в Условии недостаточно данных : для вычисления мощности надо знать либо среднюю ёмкость C0 конденсатора, либо площадь его пластин а также среднюю d0 .
Механическое изменение расстояния м-ду пластинами означает, что ёмкость данного конденсатора мизерна: менее 200 пФ, а частота вибрации пластины также ограничена ультра-звуком. При таком сочетании ограничений можно получить лишь такую микро-мощность, что от этих нано-Ватт нет никакой практической пользы. Кто сочинил для Вас эту горе-задачу? Наверное контора Сириус?
В Вашей задаче ключ К - это мусор. Его можно сразу выбросить заменой ключа на эл-схеме перемычкой. Потому что согласно Условию этот ключ замкнули и поехали дальше (искать приключений).
А дальше изменение расстояния м-ду пластинами конденсатора изменяет его ёмкость C = q / U .
При неизменном U = E от изменения C мы получаем изменение зарядов q(t) = U*C(t) = E*C(t) .
А перетекание зарядов по контуру цепи - есть переменный ток, который греет (теоретически) резистор R , на котором и выделяется искомая тепловая мощность.
Однако, в Условии недостаточно данных : для вычисления мощности надо знать либо среднюю ёмкость C0 конденсатора, либо площадь его пластин а также среднюю d0 .
Механическое изменение расстояния м-ду пластинами означает, что ёмкость данного конденсатора мизерна: менее 200 пФ, а частота вибрации пластины также ограничена ультра-звуком. При таком сочетании ограничений можно получить лишь такую микро-мощность, что от этих нано-Ватт нет никакой практической пользы. Кто сочинил для Вас эту горе-задачу? Наверное контора Сириус?
07.01.2022, 18:59
общий
ЭТО Физтех 1991 (я считаю у них качественные задачи)
ответ должен быть (ЕА)^2/(2R)
в другом варианте по такому закону меняется С и получается ответ. А в этом до чего-то пока не додумался
ответ должен быть (ЕА)^2/(2R)
в другом варианте по такому закону меняется С и получается ответ. А в этом до чего-то пока не додумался
08.01.2022, 09:51
общий
Адресаты:
Вы писали "Физтех 1991 … я считаю у них качественные задачи" - я согласен с Вами. Но с другой стороны, за более чем 40 лет практики я множество раз убеждался в пропорциональной зависимости ёмкости конденсатора и величиной переменного тока ч-з него. Независимость тока от ёмкости в Вашей задаче непривычно шокирует меня. Попробую порешать…
А Вы пожалуйста покажите Условие того другого варианта точно-дословно, где ответ (ЕА)^2/R . Может, тот вариант отличается от Вашего, но Вы сочли это отличие НЕсущественным?
А Вы пожалуйста покажите Условие того другого варианта точно-дословно, где ответ (ЕА)^2/R . Может, тот вариант отличается от Вашего, но Вы сочли это отличие НЕсущественным?
09.01.2022, 14:10
общий
Адресаты:
В учебной статье "Электроёмкость. Конденсаторы" (Ссылка1) находим формулу ёмкости плоского конденсатора:
C = [$949$]0·S / d . В большинстве задач с RC-цепями ёмкость неизменна, меняются напряжение на конденсаторе и соответственно заряд q / C·U на его обкладках. Связь этих изменений хорошо описана в статье "Переходные процессы в линейных электрических цепях. Классический метод анализа"
Все расчёты переходных процессов в RC-цепях основаны на 2м законе коммутации "Напряжение на конденсаторе не может изменяться мгновенно". Этот закон - отправная точка для "нормальных" задач с неизменной ёмкостью. В Вашей НЕтипичной задаче (шиворот-навыворот) получается наоборот: Ёмкость конденсатора менятся изза изменения расстояния между пластинами, и изза этого напряжение м-ду обкладками конденсатора изменяется сразу в начале переходного процесса. Именно это НЕтипичное напряжение "толкает" ток ч-з R. Другого источника у нас тут нет, тк Источник ЭДС E отработал сразу после замыкания ключа К , и в стационарном режиме конденсатор больше не пропускает постоянный ток.
Расшифруем доп-Условие 2·[$960$] / [$969$] << [$964$] : в нём 2·[$960$] / [$969$] = T - это период колебаний, а [$964$] = R·C - постоянная времени RC-цепи.
И тогда условие T << [$964$] надо толковать так, что в задаче надо рассматривать столь большие значения используемых R·C , которые соответствуют самому началу переходного процесса, и что этот процесс не доходит даже до середины, и начинается новый полу-период колебания. То есть : Конденсатор НЕ успевает сколь-нибудь заметно изменить свой заряд в течение полу-периода колебания.
 Считаем: Ёмкость плоского конденсатора в воздухе C = [$949$]0·S / d , где S - площадь каждой пластины, d - расстояние м-ду ними,
Считаем: Ёмкость плоского конденсатора в воздухе C = [$949$]0·S / d , где S - площадь каждой пластины, d - расстояние м-ду ними,
[$949$]0 = 8,854·10-12 Ф/м - электрическая постоянная.
Средний за период заряд конденсатора равен q0 = C·U = [$949$]0·S·E / d - это заряд в некоторый момент времени t = 0 , но в стационарном режиме, то есть когда закон расстояния
d(t) = d0·[1 + A·sin([$969$]·t)] находится в нулевой синус-фазе sin(0) = 0 .
МиниЗаряд конденсатора qm = [$949$]0·S·E / {d0·[1 + A·sin([$969$]·t)]] = [$949$]0·S·E / [d0·(1 + A)] в момент t = T/4 , в макси-синус-фазе sin(T/4) = 1 .
Разность зарядов [$916$]q = q0 - qm = [$949$]0·S·E / d - [$949$]0·S·E / [d0·(1 + A)] = ([$949$]0·S·E / d)·[(1 + A) - 1] = [$949$]0·S·E·A / d = C·E·A
Амплитуда переменного напряжения на обкладках конденсатора Um = [$916$]q / C = C·E·A / C = E·A
Поскольку задано "Внутренним сопротивлением батареи пренебречь", а ключ K работает как перемычка в стационарном режиме, значит, всё это переменное напряжение приложено к резистору R .
Форма этого напряжения почти синусоидальна при А << 1 , но синусоида заметно искажается при A > 0,01.
Синусоидальное напряжение с амплитудой Um выделяет в резисторе R мощность
P = Um2 / (2·R) = (E·A)2 / (2·R) . Получилось почти как в желаемом Вами Ответе. Только Вы потеряли множитель 2 в знаменателе. Удивляет НЕзависимость результата от абсолютного значения ёмкости конденсатора (в тч его габаритов), и при этом сильная (квадратичная!) зависимость от относительного изменения "A" ёмкости в течение одного колебания.
О том, что значение достаточно большой ёмкости конденсатора не влияет на работу электро-схемы знают все инж-электроники и радио-любители: Яркий пример : Переходный конденсатор м-ду каскадами усилителя звуковой частоты. Можно увеличить эту ёмкость например в 10 раз, и от этого увеличится 10-кратно лишь милли-секундная длительность переходного процесса - будет чуть громче щелчок в момент включения усилителя.
Фокус Вашей задачи состоит в наличии 2х переходных процессов. Первый процесс происходит сразу после замыкания ключа и быстро заканчивается. Второй процесс начинается в результате изменения расстояния между пластинами конденсатора, и этот процесс - нескочаемый, потому что по Условию T << [$964$] .
Я был столь удивлён неожиданным результатом, что сделал проверку в популярном приложении Маткад (ссылка3), где я задал максимально-реальные значения для получения макси-заметной мощности. Маткад выдал большую погрешность нестыковки с выше-полученной теоретической формулой получения амплитуды напряжения при A > 0,01 изза искажения синусоиды и смещения её постоянной составляющей
Um = (q0 - qm) / C0 . Уменьшить погрешность на порядок удалось вычислением амплитуды как половины размаха переменного напряжения:
Um = (qm - qi) / (2·C0) . Маткад-скриншот с эл-схемой прилагаю . Я добавил в скрин подробные комментарии зелёным цветом.
C = [$949$]0·S / d . В большинстве задач с RC-цепями ёмкость неизменна, меняются напряжение на конденсаторе и соответственно заряд q / C·U на его обкладках. Связь этих изменений хорошо описана в статье "Переходные процессы в линейных электрических цепях. Классический метод анализа"
Все расчёты переходных процессов в RC-цепях основаны на 2м законе коммутации "Напряжение на конденсаторе не может изменяться мгновенно". Этот закон - отправная точка для "нормальных" задач с неизменной ёмкостью. В Вашей НЕтипичной задаче (шиворот-навыворот) получается наоборот: Ёмкость конденсатора менятся изза изменения расстояния между пластинами, и изза этого напряжение м-ду обкладками конденсатора изменяется сразу в начале переходного процесса. Именно это НЕтипичное напряжение "толкает" ток ч-з R. Другого источника у нас тут нет, тк Источник ЭДС E отработал сразу после замыкания ключа К , и в стационарном режиме конденсатор больше не пропускает постоянный ток.
Расшифруем доп-Условие 2·[$960$] / [$969$] << [$964$] : в нём 2·[$960$] / [$969$] = T - это период колебаний, а [$964$] = R·C - постоянная времени RC-цепи.
И тогда условие T << [$964$] надо толковать так, что в задаче надо рассматривать столь большие значения используемых R·C , которые соответствуют самому началу переходного процесса, и что этот процесс не доходит даже до середины, и начинается новый полу-период колебания. То есть : Конденсатор НЕ успевает сколь-нибудь заметно изменить свой заряд в течение полу-периода колебания.

[$949$]0 = 8,854·10-12 Ф/м - электрическая постоянная.
Средний за период заряд конденсатора равен q0 = C·U = [$949$]0·S·E / d - это заряд в некоторый момент времени t = 0 , но в стационарном режиме, то есть когда закон расстояния
d(t) = d0·[1 + A·sin([$969$]·t)] находится в нулевой синус-фазе sin(0) = 0 .
МиниЗаряд конденсатора qm = [$949$]0·S·E / {d0·[1 + A·sin([$969$]·t)]] = [$949$]0·S·E / [d0·(1 + A)] в момент t = T/4 , в макси-синус-фазе sin(T/4) = 1 .
Разность зарядов [$916$]q = q0 - qm = [$949$]0·S·E / d - [$949$]0·S·E / [d0·(1 + A)] = ([$949$]0·S·E / d)·[(1 + A) - 1] = [$949$]0·S·E·A / d = C·E·A
Амплитуда переменного напряжения на обкладках конденсатора Um = [$916$]q / C = C·E·A / C = E·A
Поскольку задано "Внутренним сопротивлением батареи пренебречь", а ключ K работает как перемычка в стационарном режиме, значит, всё это переменное напряжение приложено к резистору R .
Форма этого напряжения почти синусоидальна при А << 1 , но синусоида заметно искажается при A > 0,01.
Синусоидальное напряжение с амплитудой Um выделяет в резисторе R мощность
P = Um2 / (2·R) = (E·A)2 / (2·R) . Получилось почти как в желаемом Вами Ответе. Только Вы потеряли множитель 2 в знаменателе. Удивляет НЕзависимость результата от абсолютного значения ёмкости конденсатора (в тч его габаритов), и при этом сильная (квадратичная!) зависимость от относительного изменения "A" ёмкости в течение одного колебания.
О том, что значение достаточно большой ёмкости конденсатора не влияет на работу электро-схемы знают все инж-электроники и радио-любители: Яркий пример : Переходный конденсатор м-ду каскадами усилителя звуковой частоты. Можно увеличить эту ёмкость например в 10 раз, и от этого увеличится 10-кратно лишь милли-секундная длительность переходного процесса - будет чуть громче щелчок в момент включения усилителя.
Фокус Вашей задачи состоит в наличии 2х переходных процессов. Первый процесс происходит сразу после замыкания ключа и быстро заканчивается. Второй процесс начинается в результате изменения расстояния между пластинами конденсатора, и этот процесс - нескочаемый, потому что по Условию T << [$964$] .
Я был столь удивлён неожиданным результатом, что сделал проверку в популярном приложении Маткад (ссылка3), где я задал максимально-реальные значения для получения макси-заметной мощности. Маткад выдал большую погрешность нестыковки с выше-полученной теоретической формулой получения амплитуды напряжения при A > 0,01 изза искажения синусоиды и смещения её постоянной составляющей
Um = (q0 - qm) / C0 . Уменьшить погрешность на порядок удалось вычислением амплитуды как половины размаха переменного напряжения:
Um = (qm - qi) / (2·C0) . Маткад-скриншот с эл-схемой прилагаю . Я добавил в скрин подробные комментарии зелёным цветом.
09.01.2022, 17:46
общий
Спасибо за решение и подробное объяснение
но непонятно как получился ответ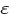 0·S·E·A / d в этом преобразовании: Разность зарядов
0·S·E·A / d в этом преобразовании: Разность зарядов 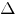 q = q0 - qm =
q = q0 - qm = 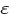 0·S·E / d -
0·S·E / d - 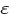 0·S·E / [d0·(1 + A)] = (
0·S·E / [d0·(1 + A)] = (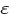 0·S·E / d)·[(1 + A) - 1] =
0·S·E / d)·[(1 + A) - 1] = 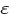 0·S·E·A / d = C·E·A
0·S·E·A / d = C·E·A
у меня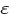 0·S·E·A / [d0(1+A)]
0·S·E·A / [d0(1+A)]
но непонятно как получился ответ
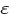 0·S·E·A / d в этом преобразовании: Разность зарядов
0·S·E·A / d в этом преобразовании: Разность зарядов 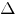 q = q0 - qm =
q = q0 - qm = 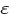 0·S·E / d -
0·S·E / d - 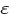 0·S·E / [d0·(1 + A)] = (
0·S·E / [d0·(1 + A)] = (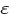 0·S·E / d)·[(1 + A) - 1] =
0·S·E / d)·[(1 + A) - 1] = 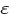 0·S·E·A / d = C·E·A
0·S·E·A / d = C·E·Aу меня
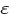 0·S·E·A / [d0(1+A)]
0·S·E·A / [d0(1+A)]
09.01.2022, 17:53
общий
Вот условие и решение задачи из другого варианта, в котором емкость меняется по закону C(t) = С0(1+Asin 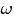 t)
t)
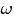 t)
t)
Прикрепленные файлы:
10.01.2022, 03:55
общий
Адресаты:
Вы спрашивали "как получился ответ [$949$]0·S·E·A / d в этом преобразовании … у меня [$949$]0·S·E·A / [d0·(1+A)]" - я старался объяснять подробно, но в данной операции я забыл пояснить замену, прошу прощения.
C = [$949$]0·S / d - это формула ёмкости плоского конденсатора для изделия с расстоянием d м-ду пластинами. Из неё вытекает формула ёмкости конденсатора Cm для изделия с расстоянием d0·(1+A) м-ду пластинами:
Cm = [$949$]0·S / [d0·(1+A)]
Тогда Ваше [$949$]0·S·E·A / [d0(1+A)] = Cm·E·A , это - Разность зарядов [$916$]q = q0 - qm .
Амплитуда переменного напряжения на обкладках конденсатора Um = [$916$]q / C = Cm·E·A / C [$8776$] E·A , потому что Cm [$8776$] C при малых A < 0,01 .
При больших значениях 0,01 < A < 1 форма результирующего переменного напряжения уже НЕ есть чисто синусоидальная, потому что синус задан в знаменателе Вашего варианта. Отсюда следует погрешность, увеличивающ-ся при возрастании A-значения.
Спасибо Вам за "условие и решение задачи из другого варианта". Там синус задан в числителе, и поэтому синусоида НЕ переворачивается и не искажается, как в Вашем, более трудном варианте.
C = [$949$]0·S / d - это формула ёмкости плоского конденсатора для изделия с расстоянием d м-ду пластинами. Из неё вытекает формула ёмкости конденсатора Cm для изделия с расстоянием d0·(1+A) м-ду пластинами:
Cm = [$949$]0·S / [d0·(1+A)]
Тогда Ваше [$949$]0·S·E·A / [d0(1+A)] = Cm·E·A , это - Разность зарядов [$916$]q = q0 - qm .
Амплитуда переменного напряжения на обкладках конденсатора Um = [$916$]q / C = Cm·E·A / C [$8776$] E·A , потому что Cm [$8776$] C при малых A < 0,01 .
При больших значениях 0,01 < A < 1 форма результирующего переменного напряжения уже НЕ есть чисто синусоидальная, потому что синус задан в знаменателе Вашего варианта. Отсюда следует погрешность, увеличивающ-ся при возрастании A-значения.
Спасибо Вам за "условие и решение задачи из другого варианта". Там синус задан в числителе, и поэтому синусоида НЕ переворачивается и не искажается, как в Вашем, более трудном варианте.
10.01.2022, 05:45
общий
Адресаты:
Если Вы - такой же зануда, каким был я сразу после института, и предпочитаете точность простоте, тогда можете, используя опыт Маткад-сверки, уменьшить влияние погрешности изза смещения постоянной составляющей при больших A-значениях.
Получим амплитуду переменного напряжения не как отклонение от постоянки, а как полу-размах амплитуд крайних значений:
[$916$]Q = [$949$]0·S·E / [d0·(1-A)] - [$949$]0·S·E / [d0·(1+A)] = [$949$]0·S·E·[(1+A) - (1-A)] / [d0·(1+A)·(1-A)] = 2·Cср·E·A ,
Um = [$916$]Q / (2·C) [$8776$] E·A
где Cср = [$949$]0·S / [d0·(1-A2)] [$8776$] [$949$]0·S / d0 = C0 с гораздо мЕньшей погрешностью, чем Cm [$8776$] C0 , тк 1 - A2 [$8776$] 1 при A < 0,1 .
Если же Вы попытаетесь полностью отбросить упрощения, то получите вместо простого ответа
P = (E·A)2 / (2·R) очень громоздкую формулу, в которой повышается риск запутаться и получить ошибку.
Уважаемые преподаватели таганрогского радио-института много-кратно советовали нам, студентам: Тренируйте своё умение упрощать формулы/вычисления до приемлемой точности, которая на производстве бывает обычно 20 %. Тогда Вы сможете выполнять свою работу высоко-производительно и с мЕньшим числом ошибок. И я всю трудовую жизнь благодарил в душе своих наставников.
Получим амплитуду переменного напряжения не как отклонение от постоянки, а как полу-размах амплитуд крайних значений:
[$916$]Q = [$949$]0·S·E / [d0·(1-A)] - [$949$]0·S·E / [d0·(1+A)] = [$949$]0·S·E·[(1+A) - (1-A)] / [d0·(1+A)·(1-A)] = 2·Cср·E·A ,
Um = [$916$]Q / (2·C) [$8776$] E·A
где Cср = [$949$]0·S / [d0·(1-A2)] [$8776$] [$949$]0·S / d0 = C0 с гораздо мЕньшей погрешностью, чем Cm [$8776$] C0 , тк 1 - A2 [$8776$] 1 при A < 0,1 .
Если же Вы попытаетесь полностью отбросить упрощения, то получите вместо простого ответа
P = (E·A)2 / (2·R) очень громоздкую формулу, в которой повышается риск запутаться и получить ошибку.
Уважаемые преподаватели таганрогского радио-института много-кратно советовали нам, студентам: Тренируйте своё умение упрощать формулы/вычисления до приемлемой точности, которая на производстве бывает обычно 20 %. Тогда Вы сможете выполнять свою работу высоко-производительно и с мЕньшим числом ошибок. И я всю трудовую жизнь благодарил в душе своих наставников.
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.



