[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-39 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1677.5,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T12:39:57.9304875+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6553,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5698},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-26T09:04:07","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-39 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.074,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T12:39:57.9307684+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5585,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-39 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.642,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T12:39:57.9308801+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5270,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-39 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":387.226,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T12:39:57.931002+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2443,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-39 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.379,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T12:39:57.9311116+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2721,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-39 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.213,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-26T12:39:57.9312533+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5712,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-24T14:38:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 201849
07.12.2021, 15:15
0.00 руб.
0
13
1
Здравствуйте! У меня возникли сложности с таким вопросом:
В цилиндр вписан прямоугольный параллелепипед, большая сторона основания которого равна а. Диагональ параллелепипеда составляет с его большей боковой гранью угол ? а с плоскостью основания угол ?. Найти площадь боковой поверхности цилиндра.
В цилиндр вписан прямоугольный параллелепипед, большая сторона основания которого равна а. Диагональ параллелепипеда составляет с его большей боковой гранью угол ? а с плоскостью основания угол ?. Найти площадь боковой поверхности цилиндра.
Обсуждение
09.12.2021, 03:20
общий
Адресаты:
Разве Вы не видите, что устаревшая программа сервера rfpro.ru исказила Ваши греческие буквы? Как понимать Ваше равнодушное бездействие?
Если задача не нужна Вам, тогда надо культурно сообщить об этом, чтоб эксперты не тратили на неё время и внимание.
А если нужна, тогда для ввода греческих букв, радикалов, интегралов показателей степени, нижних индексов… используйте BBCode rfpro.ru/help/services#510 Ссылка . Для этого в ниже-абзаце "Сообщение в мини-форум" кликните большую белую плюс-пиктограмму на зелёном фоне. Сервер откроет Вам ДопПанель спец-символов. При наведении на любой из них мышь-курсора всплывает подсказка. Потренируйтесь, введите какую-нибудь пробную бессмыслицу, но жмите не "Отправить", а "Предпросмотр". Тогда сервер покажет Вам 2 панели : Отображаемый результат и снова поле с кодами.
Нажимать Предпросмотр можно многократно. Когда Ваш Отображаемый результат понравится Вам, жмите "Отправить" для публикации.
Если Вы - пожилая мадам, очень далёкая от компьютерных приёмов работы, то Вы можете написать названия греческих букв рус-буквами: альфа, бэта, фи…
Если задача не нужна Вам, тогда надо культурно сообщить об этом, чтоб эксперты не тратили на неё время и внимание.
А если нужна, тогда для ввода греческих букв, радикалов, интегралов показателей степени, нижних индексов… используйте BBCode rfpro.ru/help/services#510 Ссылка . Для этого в ниже-абзаце "Сообщение в мини-форум" кликните большую белую плюс-пиктограмму на зелёном фоне. Сервер откроет Вам ДопПанель спец-символов. При наведении на любой из них мышь-курсора всплывает подсказка. Потренируйтесь, введите какую-нибудь пробную бессмыслицу, но жмите не "Отправить", а "Предпросмотр". Тогда сервер покажет Вам 2 панели : Отображаемый результат и снова поле с кодами.
Нажимать Предпросмотр можно многократно. Когда Ваш Отображаемый результат понравится Вам, жмите "Отправить" для публикации.
Если Вы - пожилая мадам, очень далёкая от компьютерных приёмов работы, то Вы можете написать названия греческих букв рус-буквами: альфа, бэта, фи…
09.12.2021, 16:55
общий
В цилиндр вписан прямоугольный параллелепипед, большее ребро его основания которого равна а. Диагональ параллелепипеда составляет с его большей боковой гранью угол бета, а с плоскостью основания угол альфа. Найти площадь боковой поверхности цилиндра.
09.12.2021, 17:16
общий
В цилиндр вписан прямоугольный параллелепипед, большее ребро его основания которого равна а. Диагональ параллелепипеда составляет с его большей боковой гранью угол 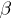 , а с плоскостью основания угол
, а с плоскостью основания угол 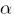 . Найти площадь боковой поверхности цилиндра.
. Найти площадь боковой поверхности цилиндра.
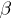 , а с плоскостью основания угол
, а с плоскостью основания угол 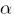 . Найти площадь боковой поверхности цилиндра.
. Найти площадь боковой поверхности цилиндра.
10.12.2021, 02:04
общий
Адресаты:
Вы хорошо постарались! Я понял Условие Вашей задачи и начинаю искать подходящие формулы для её решения. Вы можете ускорить мой поиск, если сообщите: Откуда Вы взяли эту задачу и Какую тему Вы сейчас изучаете? Вероятно, "Уравнение Плоскости в пространстве?"
Будет очень хорошо, если Вы опубликуете сюда "Методическое пособие" ("методичку") Вашего учебного заведения либо ссылку на него. Иначе я могу решить эту задачу не тем методом, который желает увидеть Ваш преподаватель.
Будет очень хорошо, если Вы опубликуете сюда "Методическое пособие" ("методичку") Вашего учебного заведения либо ссылку на него. Иначе я могу решить эту задачу не тем методом, который желает увидеть Ваш преподаватель.
10.12.2021, 15:54
общий
Адресаты:
Мне удалось решить Вашу задачу в популярном приложении Маткад (ссылка) . Но Вашему преподавателю вряд ли понравится такое Решение.
Я поискал в интернете "Геометрия Атанасян 10-11 класс", чтоб скачать указанный Вами учебник. Найти учебник целиком не удалось. Но среди огромной кучи мерзких реклам есть перечень задач из Атанасян-учебника. Их там сотни!
Какой номер Вашей задачи?
Даны ли Вам конкретные числовые данные для углов [$945$], [$946$] и длины ребра "a" ?
Я поискал в интернете "Геометрия Атанасян 10-11 класс", чтоб скачать указанный Вами учебник. Найти учебник целиком не удалось. Но среди огромной кучи мерзких реклам есть перечень задач из Атанасян-учебника. Их там сотни!
Какой номер Вашей задачи?
Даны ли Вам конкретные числовые данные для углов [$945$], [$946$] и длины ребра "a" ?
10.12.2021, 19:42
общий
этой задачи в учебнике нет. Ее придумал сам учитель. Числовых данных тоже нет.
11.12.2021, 09:35
общий
Адресаты:
Мне думается, Вы обманываете меня сообщением, будто Ваша задача взята из обычной школьной программы. В школьных учебниках задачи тщательно подобраны, они имеют посильную трудность, соответствуют пройденному учебному материалу и поэтому процесс их Решения тренирует навыки учащихся.
Из Вашей поправки "Ее придумал сам учитель" можно догадаться, что задачу сляпали горе-репетиторы из конторы "Сириус", где ничему не учат, а задают непрактичные задачи повышенной трудности. Ученики не могут решить их и перекладывают непосильный труд на экспертов портала rfpro.ru и др спецов. Пользы от этого никому нет, только убиваем время.
Я уже приступил оформлять Ответ с Решением Вашей задачи, но не знаю, как объяснить школьнику вычисление угла м-ду прямой и плоскостью в 3х-мерном пространстве, где диагональ параллелограмма имеет косые углы сразу к 2м плоскостям. Пытаюсь начертить 3х-мерный чертёж, но я давно не делал этого. Мне понадобится ещё примерно 6 часов.
Из Вашей поправки "Ее придумал сам учитель" можно догадаться, что задачу сляпали горе-репетиторы из конторы "Сириус", где ничему не учат, а задают непрактичные задачи повышенной трудности. Ученики не могут решить их и перекладывают непосильный труд на экспертов портала rfpro.ru и др спецов. Пользы от этого никому нет, только убиваем время.
Я уже приступил оформлять Ответ с Решением Вашей задачи, но не знаю, как объяснить школьнику вычисление угла м-ду прямой и плоскостью в 3х-мерном пространстве, где диагональ параллелограмма имеет косые углы сразу к 2м плоскостям. Пытаюсь начертить 3х-мерный чертёж, но я давно не делал этого. Мне понадобится ещё примерно 6 часов.
11.12.2021, 14:57
общий
это ответ
Условие: БОльшая сторона основания вписанного прямоугольного параллелепипеда = "а",
Диагональ параллелепипеда составляет с его бОльшей боковой гранью угол [$946$] , а с плоскостью основания угол [$945$] .
Вычислить площадь боковой поверхности цилиндра.
Решение: Сложные геометрические задачи надо решать с чертежом (прилагаю его ниже). Обозначим нижнее основание параллелепипеда буквами ABCD, а верхнее основание - A'B'C'D'. БОльшее ребро основания равно AD = a по Условию. Тогда BD = d - диаметр описывающего цилиндра высотой h .
В треугольнике BB'D замечаем связь: BD / B'D = cos([$945$]) . Значит Диагональ параллелепипеда B'D = d / cos([$945$])
Самое трудное: "Диагональ параллелепипеда составляет с его бОльшей боковой гранью угол [$946$]" - смотрим на плоскость бОльшей боковой грани AA'D'D . Плоскость треугольника A'B'D перпендикулярна плоскости AA'D'D. Значит, диагональ A'D есть проекция диагонали B'D на плоскость грани AA'D'D. Тогда угол м-ду диагональю параллелепипеда B'D и боковой гранью AA'D'D будет угол м-ду диагональю B'D и её проекцией A'D на грань. То есть:
sin([$946$]) = A'B' / B'D , откуда следует A'B' = B'D·sin([$946$]) [$8658$] A'B'2 = B'D2·sin2([$946$])
 По теореме Пифагора A'B'2 = AB2 = BD2 - AD2 = d2 - a2
По теореме Пифагора A'B'2 = AB2 = BD2 - AD2 = d2 - a2
Отсюда : d2 - a2 = B'D2·sin2([$946$]) . Вспоминаем, что B'D = d / cos([$945$]) , значит:
d2 - a2 = d2·sin2([$946$]) / cos2([$945$])
Чтоб решить полученное уравнение с одним неизвестным d , перемещаем члены с "d" в левую часть уравнения:
d2 - d2·sin2([$946$]) / cos2([$945$]) = a2
d2·[1 - sin2([$946$]) / cos2([$945$])] = a2
d = a / [$8730$][1 - sin2([$946$]) / cos2([$945$])] = a·cos([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]
Для вычисления искомой площади боковой поверхности цилиндра по известной формуле S = [$960$]·d·h нам осталось вычислить h-высоту цилиндра. Подмечаем, что
BB' / BD = tg([$945$]) , значит h = BB' = BD·tg([$945$]) = d·tg([$945$]) = a·cos([$945$])·tg([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])] = a·sin([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]
S = [$960$]·d·h = [$960$]·{a·cos([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]}·{a·sin([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]} = [$960$]·a2·sin([$945$])·cos([$945$]) / [cos2([$945$]) - sin2([$946$])]2
Для оптимизации результата вспомним тригонометрические упрощения: 2·sin([$945$])·cos([$945$]) = sin(2·[$945$]) ,
2·cos2([$945$]) = 1+cos(2·[$945$]) , 2·sin2([$946$]) = 1-cos(2·[$946$]) .
Ответ: Площадь боковой поверхности цилиндра равна [$960$]·a2·sin(2·[$945$]) / [cos(2·[$945$]) + cos(2·[$946$])]
Для проверки расположим наш параллелепипед на прямоугольную систему координат так, чтобы его нижняя вершина A совместилась с началом координат. Тогда плоскость xAy с нижней гранью ABCD основания имеет уравнение z = 0 , а её вектор нормали nz{0; 0; 1}.
БОльшая боковая грань AA'D'D находится на плоскости xAz с уравнением y = 0 и нормаль-вектором ny{0; 1; 0}.
Читаем пункт "Как найти угол м-ду прямой и плоскостью?" в учебной статье "Взаимное расположени прямой и плоскости. Основные задачи на прямую и плоскость" Ссылка1
Используем формулу синуса угла м-ду прямой и плоскостью:
sin([$966$]) = |n[$8594$]·p[$8594$]| / (|n|·|p|) , где n[$8594$] - нормаль-вектор плоскости, |n| - его модуль, p[$8594$] - направляющий вектор прямой, |p| - его модуль.
Я сделал вычисления в популярном приложении Маткад (ссылка2) . Маткад-скриншот с чертежом прилагаю . Я добавил в скрин подробные комментарии зелёным цветом.
Оба метода решения (Школьно-классический и Аналитической геометрии) возвратили одинаковые результаты. Значит, проверка успешна.
Примечание: в этой задаче существуют жёсткие ограничения на область допустимых значений углов. Можно задавать только такие пары углов, при которых выражения под радикалами знаменателя положительны. Успешно опробовани пары ([$945$]=[$960$]/6, [$946$]=[$960$]/6), ([$945$]=[$960$]/4, [$946$]=[$960$]/6), ([$945$]=[$960$]/6, [$946$]=[$960$]/4), ([$945$]=[$960$]/3, [$946$]=[$960$]/12) .
Я старался начертить и объяснить всё подробно и доходчиво. Если что-то осталось непонятным, задавайте вопросы в миниформуме. =Удачи!
Диагональ параллелепипеда составляет с его бОльшей боковой гранью угол [$946$] , а с плоскостью основания угол [$945$] .
Вычислить площадь боковой поверхности цилиндра.
Решение: Сложные геометрические задачи надо решать с чертежом (прилагаю его ниже). Обозначим нижнее основание параллелепипеда буквами ABCD, а верхнее основание - A'B'C'D'. БОльшее ребро основания равно AD = a по Условию. Тогда BD = d - диаметр описывающего цилиндра высотой h .
В треугольнике BB'D замечаем связь: BD / B'D = cos([$945$]) . Значит Диагональ параллелепипеда B'D = d / cos([$945$])
Самое трудное: "Диагональ параллелепипеда составляет с его бОльшей боковой гранью угол [$946$]" - смотрим на плоскость бОльшей боковой грани AA'D'D . Плоскость треугольника A'B'D перпендикулярна плоскости AA'D'D. Значит, диагональ A'D есть проекция диагонали B'D на плоскость грани AA'D'D. Тогда угол м-ду диагональю параллелепипеда B'D и боковой гранью AA'D'D будет угол м-ду диагональю B'D и её проекцией A'D на грань. То есть:
sin([$946$]) = A'B' / B'D , откуда следует A'B' = B'D·sin([$946$]) [$8658$] A'B'2 = B'D2·sin2([$946$])

Отсюда : d2 - a2 = B'D2·sin2([$946$]) . Вспоминаем, что B'D = d / cos([$945$]) , значит:
d2 - a2 = d2·sin2([$946$]) / cos2([$945$])
Чтоб решить полученное уравнение с одним неизвестным d , перемещаем члены с "d" в левую часть уравнения:
d2 - d2·sin2([$946$]) / cos2([$945$]) = a2
d2·[1 - sin2([$946$]) / cos2([$945$])] = a2
d = a / [$8730$][1 - sin2([$946$]) / cos2([$945$])] = a·cos([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]
Для вычисления искомой площади боковой поверхности цилиндра по известной формуле S = [$960$]·d·h нам осталось вычислить h-высоту цилиндра. Подмечаем, что
BB' / BD = tg([$945$]) , значит h = BB' = BD·tg([$945$]) = d·tg([$945$]) = a·cos([$945$])·tg([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])] = a·sin([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]
S = [$960$]·d·h = [$960$]·{a·cos([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]}·{a·sin([$945$]) / [$8730$][cos2([$945$]) - sin2([$946$])]} = [$960$]·a2·sin([$945$])·cos([$945$]) / [cos2([$945$]) - sin2([$946$])]2
Для оптимизации результата вспомним тригонометрические упрощения: 2·sin([$945$])·cos([$945$]) = sin(2·[$945$]) ,
2·cos2([$945$]) = 1+cos(2·[$945$]) , 2·sin2([$946$]) = 1-cos(2·[$946$]) .
Ответ: Площадь боковой поверхности цилиндра равна [$960$]·a2·sin(2·[$945$]) / [cos(2·[$945$]) + cos(2·[$946$])]
Для проверки расположим наш параллелепипед на прямоугольную систему координат так, чтобы его нижняя вершина A совместилась с началом координат. Тогда плоскость xAy с нижней гранью ABCD основания имеет уравнение z = 0 , а её вектор нормали nz{0; 0; 1}.
БОльшая боковая грань AA'D'D находится на плоскости xAz с уравнением y = 0 и нормаль-вектором ny{0; 1; 0}.
Читаем пункт "Как найти угол м-ду прямой и плоскостью?" в учебной статье "Взаимное расположени прямой и плоскости. Основные задачи на прямую и плоскость" Ссылка1
Используем формулу синуса угла м-ду прямой и плоскостью:
sin([$966$]) = |n[$8594$]·p[$8594$]| / (|n|·|p|) , где n[$8594$] - нормаль-вектор плоскости, |n| - его модуль, p[$8594$] - направляющий вектор прямой, |p| - его модуль.
Я сделал вычисления в популярном приложении Маткад (ссылка2) . Маткад-скриншот с чертежом прилагаю . Я добавил в скрин подробные комментарии зелёным цветом.
Оба метода решения (Школьно-классический и Аналитической геометрии) возвратили одинаковые результаты. Значит, проверка успешна.
Примечание: в этой задаче существуют жёсткие ограничения на область допустимых значений углов. Можно задавать только такие пары углов, при которых выражения под радикалами знаменателя положительны. Успешно опробовани пары ([$945$]=[$960$]/6, [$946$]=[$960$]/6), ([$945$]=[$960$]/4, [$946$]=[$960$]/6), ([$945$]=[$960$]/6, [$946$]=[$960$]/4), ([$945$]=[$960$]/3, [$946$]=[$960$]/12) .
Я старался начертить и объяснить всё подробно и доходчиво. Если что-то осталось непонятным, задавайте вопросы в миниформуме. =Удачи!
5
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.
