[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-53 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109944,"dynamicRating":1654.655,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-07-27T02:53:25.5463853+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6644,"questions":12,"questionsPosts":18353,"questionsAnswers":6665,"questionsPostsEvaluations":2833,"forumPosts":5699},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-07-20T05:05:12","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-53 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25767,"dynamicRating":453.889,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-07-27T02:53:25.5465467+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5677,"questions":25,"questionsPosts":7464,"questionsAnswers":1226,"questionsPostsEvaluations":789,"forumPosts":401},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-07-24T00:53:27","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-53 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":405.599,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-07-27T02:53:25.5466525+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5361,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2024-06-01T11:08:00","photo":"users/312929/bf7398e83a2a9b679ee601a457e91a12.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/312929/200_bf7398e83a2a9b679ee601a457e91a12.jpg","photoPreview120":"users/312929/120_bf7398e83a2a9b679ee601a457e91a12.jpg","photoPreview100":"users/312929/100_bf7398e83a2a9b679ee601a457e91a12.jpg","photoPreview80":"users/312929/80_bf7398e83a2a9b679ee601a457e91a12.jpg","photoPreview40":"users/312929/40_bf7398e83a2a9b679ee601a457e91a12.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-53 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":373.247,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-07-27T02:53:25.5467219+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2534,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-06-08T19:40:08","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-53 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":215.146,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-07-27T02:53:25.5468047+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2813,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-07-23T22:32:37","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-53 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":198.041,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-07-27T02:53:25.5469475+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5803,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Shvetski","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-07-05T21:42:32","photo":"users/226425/f345a2332af0cff5fba81b60c4e0d441.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/226425/200_f345a2332af0cff5fba81b60c4e0d441.jpg","photoPreview120":"users/226425/120_f345a2332af0cff5fba81b60c4e0d441.jpg","photoPreview100":"users/226425/100_f345a2332af0cff5fba81b60c4e0d441.jpg","photoPreview80":"users/226425/80_f345a2332af0cff5fba81b60c4e0d441.jpg","photoPreview40":"users/226425/40_f345a2332af0cff5fba81b60c4e0d441.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true}]
Консультация № 201082
04.06.2021, 14:29
0.00 руб.
04.06.2021, 16:00
0
5
1
Здравствуйте! Прошу помощи в следующем вопросе:
"Бесконечный тонкий прямой проводник равномерно заряжен с линейной плотностью заряда [$961$]=5*10-10Кл/м. Считая, что на расстоянии r1=1м от проводника потенциал созданного им электрического поля равен [$966$]1=20В, определить величину потенциала на расстоянии r2=e=2,72 м от проводника. 1/(4[$960$][$949$]0)=9*109Ф/м."

"Бесконечный тонкий прямой проводник равномерно заряжен с линейной плотностью заряда [$961$]=5*10-10Кл/м. Считая, что на расстоянии r1=1м от проводника потенциал созданного им электрического поля равен [$966$]1=20В, определить величину потенциала на расстоянии r2=e=2,72 м от проводника. 1/(4[$960$][$949$]0)=9*109Ф/м."

Обсуждение
04.06.2021, 22:09
общий
это ответ
ПРИМЕЧАНИЕ. Полужирным шрифтом обозначены векторы.
Найдем напряженность поля. Можно, конечно, проинтегрировать, но мы воспользуемся теоремой Гаусса для электростатической системы:
[$8747$]E[$183$]dS = [$931$]q/[$949$]0
В нашем случае из соображений симметрии следует, что вектор напряженности направлен радиально, а поверхность, на которой он имеет одинаковое значение - это цилиндр, на оси которого находится проводник.
Поскольку цилиндр бесконечный, то потоком через его торцы можно пренебречь. Формально возьмем цилиндр длиной L и радиусом R. Тогда площадь его боковой поверхности равна S = 2[$183$][$960$][$183$]r[$183$]L
На оси такого цилиндра суммарный заряд q=[$961$][$183$]L. На поверхности такого цилиндра модуль E одинаков.
Значит, по теореме Гаусса
E[$183$]S=q/[$949$]0
или
E[$183$]2[$183$][$960$][$183$]r[$183$]L = [$961$][$183$]L/[$949$]0
=> E = [$961$]/ (2[$183$][$960$][$183$][$949$]0[$183$]r) = 2[$183$][$961$]/ (4[$183$][$960$][$183$][$949$]0[$183$]r)
Обозначим С= 2[$183$][$961$]/ (4[$183$][$960$][$183$][$949$]0)
Тогда E = C/r
Теперь ищем потенциал (по сути, работу по перемещению заряда из одной точки в другую). Чтобы легче было интегрировать, движемся по радиусу.
Вычисляем интеграл с пределами от 1 до e (наши численные значения):
[$916$][$966$]=[$966$]-[$966$]0 =[$8747$]E[$183$]dr = [$8747$]C/r[$183$]dr =С[$183$]( ln(e) - ln(1) ) =C
Значит, искомое значение [$966$]=[$966$]0+С
Подставляем значения [$966$]=20+2[$183$]5[$183$]10-10[$183$]9[$183$]109 = 20 +9 = 29 (В)
ОТВЕТ: 29 В
Вроде бы, так.
Найдем напряженность поля. Можно, конечно, проинтегрировать, но мы воспользуемся теоремой Гаусса для электростатической системы:
[$8747$]E[$183$]dS = [$931$]q/[$949$]0
В нашем случае из соображений симметрии следует, что вектор напряженности направлен радиально, а поверхность, на которой он имеет одинаковое значение - это цилиндр, на оси которого находится проводник.
Поскольку цилиндр бесконечный, то потоком через его торцы можно пренебречь. Формально возьмем цилиндр длиной L и радиусом R. Тогда площадь его боковой поверхности равна S = 2[$183$][$960$][$183$]r[$183$]L
На оси такого цилиндра суммарный заряд q=[$961$][$183$]L. На поверхности такого цилиндра модуль E одинаков.
Значит, по теореме Гаусса
E[$183$]S=q/[$949$]0
или
E[$183$]2[$183$][$960$][$183$]r[$183$]L = [$961$][$183$]L/[$949$]0
=> E = [$961$]/ (2[$183$][$960$][$183$][$949$]0[$183$]r) = 2[$183$][$961$]/ (4[$183$][$960$][$183$][$949$]0[$183$]r)
Обозначим С= 2[$183$][$961$]/ (4[$183$][$960$][$183$][$949$]0)
Тогда E = C/r
Теперь ищем потенциал (по сути, работу по перемещению заряда из одной точки в другую). Чтобы легче было интегрировать, движемся по радиусу.
Вычисляем интеграл с пределами от 1 до e (наши численные значения):
[$916$][$966$]=[$966$]-[$966$]0 =[$8747$]E[$183$]dr = [$8747$]C/r[$183$]dr =С[$183$]( ln(e) - ln(1) ) =C
Значит, искомое значение [$966$]=[$966$]0+С
Подставляем значения [$966$]=20+2[$183$]5[$183$]10-10[$183$]9[$183$]109 = 20 +9 = 29 (В)
ОТВЕТ: 29 В
Вроде бы, так.
5
04.06.2021, 23:40
общий
Адресаты:
немного странно то, что мы, вроде бы, от проводника становимся дальше, а потенциал при этом увеличивается... вы не находите?  или все в порядке - не могу понять
или все в порядке - не могу понять
 или все в порядке - не могу понять
или все в порядке - не могу понять
Об авторе:
С уважением
shvetski
С уважением
shvetski
05.06.2021, 00:17
общий
Адресаты:
я пытаюсь вывести формулу из известной из школы
[$966$]=k*q/r
и составляю интеграл из треугольника
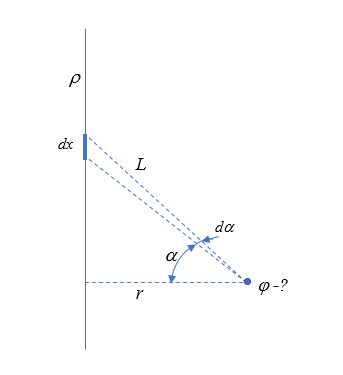
d[$966$]=k*dq/L=k[$961$]*dx/L=k[$961$]L*d[$945$]/L = k[$961$]d[$945$] - т.е., вообще от r не зависит ?
[$8658$]
[$966$]=k*[$961$]-п/2п/2[$8747$]d[$945$]=[$961$]/4[$949$]0; k=1/4[$960$][$949$]0
Не хватает что-то в мозгах, математики, помогите
Что я не так делаю?
[$966$]=k*q/r
и составляю интеграл из треугольника

d[$966$]=k*dq/L=k[$961$]*dx/L=k[$961$]L*d[$945$]/L = k[$961$]d[$945$] - т.е., вообще от r не зависит ?

[$8658$]
[$966$]=k*[$961$]-п/2п/2[$8747$]d[$945$]=[$961$]/4[$949$]0; k=1/4[$960$][$949$]0
Не хватает что-то в мозгах, математики, помогите

Что я не так делаю?
Об авторе:
С уважением
shvetski
С уважением
shvetski
05.06.2021, 02:10
общий
Адресаты:
Вы писали "странно то, что мы, вроде бы, от проводника становимся дальше, а потенциал при этом увеличивается" - Вы правы, у всех думающих людей такое представление вызывает неприятие и подозрение изза невозможности сопоставить полученный результат здравому смыслу. Я тоже споткнулся об эту чушь неск-ко лет назад, долго искал объяснение и нашёл. Цитирую (прошу извинить за сокращения, я конспектировал для себя) :
"Физич смысл имеет т-ко разность потенциалов 2х точек, поэтому потенциал, как и потенциальная энергия, определен с точностью до произвольной постоянной, связанной с выбором начала его отсчета.
Нормировка потенциала - придание однозначности потенциалу путем приписывания ему определенного значени в к-либо точке. Обычно используют один из 2х наиболее удобных способов нормировки:
1) если заряды занимают ограниченную область пространства, то принимают равным нулю значение потенциала в бесконечно удаленной точке;
2) если проводящее тело каким-то образом соединено с Землей (заземление), то его потенциал равен потенциалу Земли (потенциал Земли мож положить =0).
В модельных задачах, где заряды занимают бесконечные области (бесконечная заряженная плоскость, нить, цилиндр…), выбор нулевой точки потенциала произволен и определяется соображениями симметрии и удобством записи результата."
Вот ещё примеры "модельных задач" с пояснениями: "Электрическое поле плоскости. Жидкевич ВИ" alsak.ru/item/353-7.html ;
Определить потенциал поля rfpro.ru/question/198503
Так что не ломайте голову (она ещё пригодится Вам для более полезных задач), это причуды "модельных задач" от институтских кандидатов наук, далёких от практики и опытов с явлениями Природы.
"Физич смысл имеет т-ко разность потенциалов 2х точек, поэтому потенциал, как и потенциальная энергия, определен с точностью до произвольной постоянной, связанной с выбором начала его отсчета.
Нормировка потенциала - придание однозначности потенциалу путем приписывания ему определенного значени в к-либо точке. Обычно используют один из 2х наиболее удобных способов нормировки:
1) если заряды занимают ограниченную область пространства, то принимают равным нулю значение потенциала в бесконечно удаленной точке;
2) если проводящее тело каким-то образом соединено с Землей (заземление), то его потенциал равен потенциалу Земли (потенциал Земли мож положить =0).
В модельных задачах, где заряды занимают бесконечные области (бесконечная заряженная плоскость, нить, цилиндр…), выбор нулевой точки потенциала произволен и определяется соображениями симметрии и удобством записи результата."
Вот ещё примеры "модельных задач" с пояснениями: "Электрическое поле плоскости. Жидкевич ВИ" alsak.ru/item/353-7.html ;
Определить потенциал поля rfpro.ru/question/198503
Так что не ломайте голову (она ещё пригодится Вам для более полезных задач), это причуды "модельных задач" от институтских кандидатов наук, далёких от практики и опытов с явлениями Природы.

05.06.2021, 08:11
общий
Адресаты:
Интегрировать нужно не потенциал, а напряженность (по сути, силу), вернее, ее проекцию на радиальное направление. Тогда получите суммарную действующую силу (напряженность) в данной точке.
А потенциалы не интегрируются, а отнимаются, т.к., по сути, это работа по перемещению заряда из одной точки в другую, которая не зависит от пути, а только от начальной и конечной точки.
НАСЧЕТ СТРАННОГО ВОЗРАСТАЮЩЕГО ПОТЕНЦИАЛА.
В мире физики (математики) много "чудес". Например, бесконечно длинный равномерно заряженный проводник в этой задаче. Значит, если перемещать ВДОЛЬ него пробный заряд, чтобы уйти на бесконечность, где потенциал принимается равным нулю, у нас это никогда не получится, т.к. мы так и останемся у проводника. Кстати, суммарный заряд такого проводника, по-любому, тоже бесконечный.
Есть еще одна такая же бесконечная абстракция - бесконечная равномерно заряженная плоскость и тоже с бесконечным зарядом. Там вообще напряженность на любом расстоянии одинаковая, а значит, на бесконечности потенциал точно не упадет до нуля.
Если же рассматривать одиночный заряд и его напряженность (по сути, силу) E= k[$183$]q/r2, то [$966$] = [$8747$] E[$183$]dr вдоль радиуса как раз даст знакомое со школы выражение для потенциала [$966$] = -k[$183$]q/r + C, где выбирается C =0 при r = [$8734$].
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.

