[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1675.71,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-05-03T10:30:05.0623473+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6560,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5698},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-29T08:02:54","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":460.497,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-05-03T10:30:05.0625512+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5592,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.094,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-05-03T10:30:05.0626342+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5277,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":386.12,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-05-03T10:30:05.0626942+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2450,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":221.809,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-05-03T10:30:05.0627622+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2728,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":200.967,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-05-03T10:30:05.0629568+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5718,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-05-02T06:49:11","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 184392
06.11.2011, 16:25
65.00 руб.
06.11.2011, 19:43
0
8
3
Здравствуйте! У меня возникли сложности с таким вопросом:
Точки А1, А2, А3, А4 являются вершинами пирамиды. Вычислить:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А3А2;
3) площадь грани А1А2А3;
4) объем пирамиды;
5) уравнение прямой А1А3;
6) уравнение плоскости А2А3А4;
7) уравнение высоты, опущенной из вершины А1 на грань А2А3А4;
8) длину этой высоты.
Сделать чертеж.
А1(2;–4;–3), А2(5;–6; 0), А3(–1; 3;–3), А4(–10;–8; 7).
Точки А1, А2, А3, А4 являются вершинами пирамиды. Вычислить:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А3А2;
3) площадь грани А1А2А3;
4) объем пирамиды;
5) уравнение прямой А1А3;
6) уравнение плоскости А2А3А4;
7) уравнение высоты, опущенной из вершины А1 на грань А2А3А4;
8) длину этой высоты.
Сделать чертеж.
А1(2;–4;–3), А2(5;–6; 0), А3(–1; 3;–3), А4(–10;–8; 7).
Обсуждение

Неизвестный
06.11.2011, 16:46
общий
Точки А1, А2, А3, А4 являются вершинами пирамиды. Вычислить: 1) длину ребра А1А2; 2) угол между ребрами А1А2 и А3А2; 3) площадь грани А1А2А3; 4) объем пирамиды; 5) уравнение прямой А1А3; 6) уравнение плоскости А2А3А4; 7) уравнение высоты, опущенной из вершины А1 на грань А2А3А4; 8) длину этой высоты. Сделать чертеж.
А1(2;–4;–3), А2(5;–6; 0), А3(–1; 3;–3), А4(–10;–8; 7).
А1(2;–4;–3), А2(5;–6; 0), А3(–1; 3;–3), А4(–10;–8; 7).
06.11.2011, 16:53
общий
это ответ
Здравствуйте, Посетитель - 384181!
1)
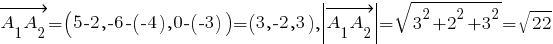
2)


3)

4)
Объем пирамиды равен смешанному произведению векторов, разделенному на 6:

Смешанное произведение равно определителю, составленному из координат этих векторов:
|3 -2 3 |
|-3 7 0 |=438
|-12 -4 10|
V=438/6=73
5)
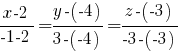

6) Приравниваем определитель к 0:
|x-5 y+6 z-0|
|-1-5 3+6 -3-0|=0
|-10-5 -8+6 7-0|
63(x-5)+12z+45(y+6)+135z-6(x-5)+42(y+6)=0
57x+87y+147z+237=0
19x+29y+39z+79=0
7)
Вектор нормали к плоскости (19,29,39)
Прямая проходит через точку А1 перпендикулярно к плоскости, то есть параллельно к нормали:
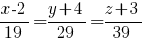
8)
Находим точку пересечения, введя параметр k:
x=19k+2, y=29k-4, z=39k-3
19(19k+2)+29(29k-4)+39(39k-3)+79=0
2723k-116=0
k=0,04 (приблизительно)
x=19*0,04+2=2,76
y=29*0,04-4=-2,84
z=39*0,04-3=-1,44
Точка пересечения А5(2,76;-2,84;-1,44)
Длина равна длине вектора А1А5:

1)
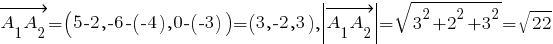
2)


3)

4)
Объем пирамиды равен смешанному произведению векторов, разделенному на 6:

Смешанное произведение равно определителю, составленному из координат этих векторов:
|3 -2 3 |
|-3 7 0 |=438
|-12 -4 10|
V=438/6=73
5)
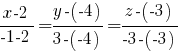

6) Приравниваем определитель к 0:
|x-5 y+6 z-0|
|-1-5 3+6 -3-0|=0
|-10-5 -8+6 7-0|
63(x-5)+12z+45(y+6)+135z-6(x-5)+42(y+6)=0
57x+87y+147z+237=0
19x+29y+39z+79=0
7)
Вектор нормали к плоскости (19,29,39)
Прямая проходит через точку А1 перпендикулярно к плоскости, то есть параллельно к нормали:
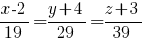
8)
Находим точку пересечения, введя параметр k:
x=19k+2, y=29k-4, z=39k-3
19(19k+2)+29(29k-4)+39(39k-3)+79=0
2723k-116=0
k=0,04 (приблизительно)
x=19*0,04+2=2,76
y=29*0,04-4=-2,84
z=39*0,04-3=-1,44
Точка пересечения А5(2,76;-2,84;-1,44)
Длина равна длине вектора А1А5:

06.11.2011, 20:19
общий
это ответ
Здравствуйте, Посетитель - 384181!
Решение 6,7 и 8 в прикрепленном файле.
Решение 6,7 и 8 в прикрепленном файле.
Прикрепленные файлы:
07.11.2011, 19:27
общий
Адресаты:
Исправьте, пожалуйста. в п. 5. Ведь y3 - y1 = 3 - (-4) = 3 + 4 = 7...

Об авторе:
Facta loquuntur.
Facta loquuntur.
07.11.2011, 20:11
общий
это ответ
Здравствуйте, Посетитель - 384181!
После того, как в Вашем распоряжении появилось решение задачи, основанное на применении формальных приёмов аналитической геометрии, уместным будет посмотреть на решение части этой задачи с объяснением, в котором используются более элементарные расчёты, без применения матричного исчисления. Ибо как показывает мой опыт, большинство студентов мало что понимает после выполнения типовых расчётов по высшей математике. Это крайне неблагоприятно сказывается на их отношении к этому предмету и не позволяет им применить методы высшей математики (и не только высшей ) при решении инженерных задач.
) при решении инженерных задач.
1. Длина ребра [A1A2] вычисляется по теореме Пифагора. Если от координат точки A2 отнять соответствующие координаты точки A1, то получим координаты вектора A[sub]1[/sub]A[sub]2[/sub], который равен разности радиус-векторов точек A2 и A1 (A[sub]1[/sub]A[sub]2[/sub] = OA[sub]2[/sub] - OA[sub]1[/sub]): A[sub]1[/sub]A[sub]2[/sub] = (5 - 2; -6 - (-4); 0 - (-3)) = (3; -2; 3), или A[sub]1[/sub]A[sub]2[/sub] = 3i - 2j + 3k. Длина этого вектора и равна искомой длине ребра: |A1A2| = |A[sub]1[/sub]A[sub]2[/sub] = [$8730$](32 + (-2)2 + 32) = [$8730$]22.
2. Рёбра [A1A2] и [A3A2] выходят из одной и той же вершины пирамиды - точки A2. Сопоставим ребру [A1A2] вектор A[sub]2[/sub]A[sub]1[/sub] = -A[sub]1[/sub]A[sub]2[/sub] = (-3; 2; -3) = -3i + 2j - 3k, а ребру [A3A2] - вектор A[sub]2[/sub]A[sub]3[/sub] = (-1 - 5; 3 - (-6); -3 - 0) = (-6; 9; -3) = -6i + 9j - 3k, длина которого |A[sub]2[/sub]A[sub]3[/sub]| = [$8730$]((-6)2 + 92 + (-3)2) = [$8730$](36 + 81 + 9) = [$8730$]126.
К сожалению, декартова прямоугольная система координат не предполагает возможности непосредственного вычисления угла между двумя векторами. Поэтому найти искомый угол можно только опосредованно - через нахождение одной из его тригонометрических функций. Такую возможность, в частности, предоставляет так называемое скалярное произведение. Воспользуемся сначала тем, что нахождение скалярного произведения двух векторов сводится к суммированию произведений их одноимённых координат. Если полученная сумма больше нуля, то угол между векторами острый. Если полученная сумма меньше нуля, то угол тупой. Если же эта сумма равна нулю, то векторы взаимно перпендикулярны.
В нашем случае A[sub]2[/sub]A[sub]1[/sub] [$183$] A[sub]2[/sub]A[sub]3[/sub] = (-3) [$183$] (-6) + 2 [$183$] 9 + (-3) [$183$] (-3) = 18 + 18 + 9 = 45.
С другой стороны, скалярное произведение двух векторов находится умножением произведения длин этих векторов на косинус угла между ними. Если обозначить данный угол буквой "[$966$]", то в нашем случае будем иметь
A[sub]2[/sub]A[sub]1[/sub] [$183$] A[sub]2[/sub]A[sub]3[/sub] = [$8730$]22 [$183$] [$8730$]126 [$183$] cos [$966$] = [$8730$](2 [$183$] 11 [$183$] 2 [$183$] 63) [$183$] cos [$966$] = 2[$8730$]693 [$183$] cos [$966$].
Приравняв правые части выражений для скалярного произведения, получим 2[$8730$]693 [$183$] cos [$966$], откуда найдём
cos [$966$] = 45/(2[$8730$]693) [$8776$] 0,8547, [$966$] [$8776$] 31[$186$] 16'.
Итак, угол между векторами A[sub]2[/sub]A[sub]1[/sub] и A[sub]2[/sub]A[sub]3[/sub] составляет примерно 31[$186$] 16'. Это значение соответствует и углу между рёбрами [A1A2] и [A3A2] пирамиды. Правда, в условии задачи требуется всё же найти угол между ребрами [А1А2] и [А3А2], что несколько меняет существо дела, но не влияет на результат.
Действительно, A[sub]2[/sub]A[sub]1[/sub] = (3; -2; 3), A[sub]2[/sub]A[sub]3[/sub] = -A[sub]3[/sub]A[sub]2[/sub] = (6; -9; 3), A[sub]1[/sub]A[sub]2[/sub] [$183$] A[sub]3[/sub]A[sub]2[/sub] = 3 [$183$] 6 + (-2) [$183$] (-9) + 3 [$183$] 3 = 18 + 18 + 9 = 45, |A[sub]1[/sub]A[sub]2[/sub]| = |A[sub]2[/sub]A[sub]1[/sub]| = [$8730$]22, |A[sub]3[/sub]A[sub]2[/sub]| = |A[sub]2[/sub]A[sub]3[/sub]| = [$8730$]126. Поэтому и угол между векторами будет иметь ту же величину.
3. Площадь S грани A1A2A3 можно найти по известной из элементарной геометрии формуле для площади треугольника, которая в нашем случае имеет следующий вид: S = 1/2 [$183$] |A[sub]2[/sub]A[sub]1[/sub]| [$183$] |A[sub]2[/sub]A[sub]3[/sub]| [$183$] sin [$966$]. Поскольку
sin [$966$] = [$8730$](1 - cos2 [$966$]) = [$8730$](1 - (45/(2[$8730$]693))2) = [$8730$](1 - 2025/2772) = [$8730$](747/2772) = [$8730$](83/308) [$8776$] 0,5191,
постольку
S = 1/2 [$149$] [$8730$]22 [$183$] [$8730$]126 [$183$] [$8730$](83/308) = [$8730$](57519/308) = [$8730$](747/4) = 3[$8730$]83/2 [$8776$] 13,67.
4. В элементарной геометрии устанавливается, что объём V пирамиды равен 1/3 произведения площади S её основания на высоту h: V = Sh/3. Примем за основание пирамиды её грань A1A2A3 и найдём высоту h. Понятно, что эта высота равна расстоянию между основанием пирамиды и вершиной A4. Найдём расстояние от точки A4 до плоскости A1A2A3.
Специально вводимое понятие векторного произведения векторов как вектора, длина которого равна произведения длин этих векторов на синус угла между ними, а направление определяется исходя из получения правой тройки, образуемых последовательностью направленных отрезков "первый отрезок - второй отрезок - векторное произведение", даёт возможность поступить следующим образом. Найдём векторное произведение векторов A[sub]2[/sub]A[sub]1[/sub] и A[sub]2[/sub]A[sub]3[/sub]:
N = A[sub]2[/sub]A[sub]1[/sub] X A[sub]2[/sub]A[sub]3[/sub] = (-3i + 2j - 3k) X (-6i + 9j - 3k) = 18(i X i) - 27(i X j) + 9(i X k) - 12(j X i) + 18(j X j) - 6(j X k) + 18(k X i) - 27(k X j) + 9(k X k) =
= 0 - 27k - 9j + 12k + 0 - 6i + 18j + 27i + 0 = 21i + 9j - 15k = (21; 9; -15).
Вектор, координаты которого мы установили, направлен перпендикулярно грани A1A2A3, а его длина составляет
|N| = [$8730$]((21)2 + 92 + (-15)2) = [$8730$](441 + 81 + 225) = [$8730$]747 = 3[$8730$]83 [$8776$] 27,33.
Поэтому вектор
n = N/|N| = (21i + 9j - 15k)/(3[$8730$]83) - единичный вектор нормали к плоскости A1A2A3.
Заметим, сравнивая результат вычисления длины векторного произведения с результатом п. 3, что в качестве "бесплатного приложения" мы продемонстрировали альтернативный способ вычисления площади грани A1A2A3: нужно найти векторное произведение векторов, на которых построена грань, и результат разделить пополам.
Отвлечёмся немного и укажем, что если умножить скалярно нормальный вектор плоскости на любой направленный отрезок, расположенный на этой плоскости, то в силу взаимной перпендикулярности сомножителей, получим нуль. Этот способ позволяет найти общее уравнение грани A1A2A3: обозначим через x, y, z координаты произвольной точки M, принадлежащей этой грани; вектор A[sub]1[/sub]M = (x - 2; y + 4; z + 3) расположен на рассматриваемой плоскости; найдём скалярное произведение
(A[sub]2[/sub]A[sub]1[/sub] X A[sub]2[/sub]A[sub]3[/sub]) [$183$] A[sub]1[/sub]M = (21; 9; -15) [$183$] (x - 2; y + 4; z + 3) = 21(x - 2) + 9(y + 4) - 15(z + 3) = 0,
21x + 9y - 15z - 42 + 36 - 45 = 0,
21x + 9y - 15z - 51 = 0 - общее уравнение плоскости A1A2A3.
"Ради интереса" подставим в полученное уравнение координаты точки A2 и проверим, удовлетворяют ли они ему:
21 [$183$] 5 + 9 [$183$] (-6) - 15 [$183$] 0 - 51 = 0,
105 - 54 - 0 - 51 = 0,
0 = 0,
как и должно быть.
Чтобы получить наглядное представление о положении плоскости A1A2A3 в пространстве с введённой на нём декартовой прямоугольной системой координат, выполним следующие тождественные преобразования общего уравнения этой плоскости:
21x + 9y - 15z - 51 = 0,
21x + 9y - 15z = 51,
(21/51)x + (9/51)y - (15/51)z = 1,
x/(51/21) + y/(51/9) + z/(-51/15) = 1,
x/(51/21) + y/(17/3) + z/(-17/5) = 1.
Получили уравнение плоскости A1A2A3 в отрезках на осях координат. Из этого уравнения следует, что рассматриваемая плоскость пересекает ось абсцисс в точке x = 51/21 [$8776$] 2,43, ось ординат - в точке y = 17/3 [$8776$] 5,67, ось аппликат - в точке z = -17/5 = -3,4. Данное обстоятельство может быть использовано при выполнении чертежа пирамиды (но на этом мы останавливаться не будем).
Для "общего развития": поскольку А4(–10;–8; 7), постольку точка А4 расположена в третьем октанте координатного пространства (если непонятно, что это значит, посмотрите здесь). В то же время нормальный вектор плоскости A1A2A3 N = (21; 9; -15) оказывается направленным из начала координат в пятый октант. Можно в качестве нормального вектора плоскости A1A2A3 взять и вектор, направленный противоположно, т. е N' = (-21; -9; 15) (вообще, любой вектор, коллинеарный вектору N, перпендикулярен плоскости A1A2A3). Он "указывает" как раз на третий октант. Единичным вектором соответствующего направления будет тогда вектор n' = (-21i - 9j + 15k)/(3[$8730$]83).
Определим теперь угол, например, между векторами N' и A[sub]1[/sub]A[sub]4[/sub] = (-10 - 2; -8 - (-4); 7 - (-3)) = (-12; -4; 10), имеющим длину
|A[sub]1[/sub]A[sub]4[/sub]| = [$8730$]((-12)2 + (-4)2 + (10)2) = [$8730$](144 + 16 + 100) = [$8730$]260 = 2[$8730$]65.
В результате скалярного умножения получим
N' [$183$] A[sub]1[/sub]A[sub]4[/sub] = (-21; -9; 15) [$183$] (-12; -4; 10) = (-21) [$183$] (-12) + (-9) [$183$] (-4) + 15 [$183$] 10 = 252 + 36 + 150 = 438,
тогда для угла [$968$] между между векторами N' и A[sub]1[/sub]A[sub]4[/sub] найдём
cos [$968$] = 438/(3[$8730$]83 [$183$] 2[$8730$]65) = 438/(6[$8730$]5395) = 219/(3[$8730$]5395) [$8776$] 0,9939,
sin [$968$] = [$8730$](1 - (219/(3[$8730$]5395))2) = [$8730$](1 - 47961/48555) = [$8730$](594/48555) [$8776$] 0,1106.
Понятно, что если вектор A[sub]1[/sub]A[sub]4[/sub] расположен под углом [$968$] к вектору N' - нормальному вектору плоскости A1A2A3, то он расположен под тем же углом и к единичному нормальному вектору n' = (-21i - 9j + 15k)/(3[$8730$]83). Но проекция вектора A[sub]1[/sub]A[sub]4[/sub] на вектор n' является высотой пирамиды, опущенной из вершины A4 на грань A1A2A3. Значит,
h = |A1A4| [$183$] cos [$968$] = 2[$8730$]65 [$183$] 219/(3[$8730$]5395) = 438/(3[$8730$]83) [$8776$] 16,03,
V = Sh/3 = 1/3 [$183$] 3[$8730$]83/2 [$183$] 438/(3[$8730$]83) = 438/6 = 73.
5. Уравнение прямой A1A3, действительно, проще всего получить в виде уравнения прямой, проходящей через две данные точки: A1 и A3. Оно же будет и каноническим уравнением этой прямой. Как было показано в ответе (исправленном) Романа Селивёрстова, получим
(x - 2)/(-3) = (y + 4)/7 = (z + 3)/0.
Выражение (z + 3)/0 не должно Вас смущать. Оно всего лишь отражает то обстоятельство, что прямая A1A3 расположена в плоскости z = -3, откуда
z + 3 = 0. (*)
Далее имеем
(x - 2)/(-3) = (y + 4)/7,
x - 2 = -3(y + 4),
x - 2 = -3y - 12,
x + 3y - 2 + 12 = 0,
x + 3y + 10 = 0. (**)
Система уравнений (*), (**) задаёт прямую A1A3 в общем виде. Уравнение (*) задаёт плоскость, перпендикулярную оси аппликат, а уравнение (**) - плоскость, параллельную этой оси.
Пункты 6, 7, 8 задания рассматривать не будем. Ответы на них могут быть получены рассмотренными выше способами.
Ниже дан чертёж пирамиды.

Если усвоены показанные способы решения, то можно перейти и к использованию матричного исчисления, которое является всего лишь более компактной формой записи этих способов.
С уважением.
После того, как в Вашем распоряжении появилось решение задачи, основанное на применении формальных приёмов аналитической геометрии, уместным будет посмотреть на решение части этой задачи с объяснением, в котором используются более элементарные расчёты, без применения матричного исчисления. Ибо как показывает мой опыт, большинство студентов мало что понимает после выполнения типовых расчётов по высшей математике. Это крайне неблагоприятно сказывается на их отношении к этому предмету и не позволяет им применить методы высшей математики (и не только высшей
 ) при решении инженерных задач.
) при решении инженерных задач.1. Длина ребра [A1A2] вычисляется по теореме Пифагора. Если от координат точки A2 отнять соответствующие координаты точки A1, то получим координаты вектора A[sub]1[/sub]A[sub]2[/sub], который равен разности радиус-векторов точек A2 и A1 (A[sub]1[/sub]A[sub]2[/sub] = OA[sub]2[/sub] - OA[sub]1[/sub]): A[sub]1[/sub]A[sub]2[/sub] = (5 - 2; -6 - (-4); 0 - (-3)) = (3; -2; 3), или A[sub]1[/sub]A[sub]2[/sub] = 3i - 2j + 3k. Длина этого вектора и равна искомой длине ребра: |A1A2| = |A[sub]1[/sub]A[sub]2[/sub] = [$8730$](32 + (-2)2 + 32) = [$8730$]22.
2. Рёбра [A1A2] и [A3A2] выходят из одной и той же вершины пирамиды - точки A2. Сопоставим ребру [A1A2] вектор A[sub]2[/sub]A[sub]1[/sub] = -A[sub]1[/sub]A[sub]2[/sub] = (-3; 2; -3) = -3i + 2j - 3k, а ребру [A3A2] - вектор A[sub]2[/sub]A[sub]3[/sub] = (-1 - 5; 3 - (-6); -3 - 0) = (-6; 9; -3) = -6i + 9j - 3k, длина которого |A[sub]2[/sub]A[sub]3[/sub]| = [$8730$]((-6)2 + 92 + (-3)2) = [$8730$](36 + 81 + 9) = [$8730$]126.
К сожалению, декартова прямоугольная система координат не предполагает возможности непосредственного вычисления угла между двумя векторами. Поэтому найти искомый угол можно только опосредованно - через нахождение одной из его тригонометрических функций. Такую возможность, в частности, предоставляет так называемое скалярное произведение. Воспользуемся сначала тем, что нахождение скалярного произведения двух векторов сводится к суммированию произведений их одноимённых координат. Если полученная сумма больше нуля, то угол между векторами острый. Если полученная сумма меньше нуля, то угол тупой. Если же эта сумма равна нулю, то векторы взаимно перпендикулярны.
В нашем случае A[sub]2[/sub]A[sub]1[/sub] [$183$] A[sub]2[/sub]A[sub]3[/sub] = (-3) [$183$] (-6) + 2 [$183$] 9 + (-3) [$183$] (-3) = 18 + 18 + 9 = 45.
С другой стороны, скалярное произведение двух векторов находится умножением произведения длин этих векторов на косинус угла между ними. Если обозначить данный угол буквой "[$966$]", то в нашем случае будем иметь
A[sub]2[/sub]A[sub]1[/sub] [$183$] A[sub]2[/sub]A[sub]3[/sub] = [$8730$]22 [$183$] [$8730$]126 [$183$] cos [$966$] = [$8730$](2 [$183$] 11 [$183$] 2 [$183$] 63) [$183$] cos [$966$] = 2[$8730$]693 [$183$] cos [$966$].
Приравняв правые части выражений для скалярного произведения, получим 2[$8730$]693 [$183$] cos [$966$], откуда найдём
cos [$966$] = 45/(2[$8730$]693) [$8776$] 0,8547, [$966$] [$8776$] 31[$186$] 16'.
Итак, угол между векторами A[sub]2[/sub]A[sub]1[/sub] и A[sub]2[/sub]A[sub]3[/sub] составляет примерно 31[$186$] 16'. Это значение соответствует и углу между рёбрами [A1A2] и [A3A2] пирамиды. Правда, в условии задачи требуется всё же найти угол между ребрами [А1А2] и [А3А2], что несколько меняет существо дела, но не влияет на результат.
Действительно, A[sub]2[/sub]A[sub]1[/sub] = (3; -2; 3), A[sub]2[/sub]A[sub]3[/sub] = -A[sub]3[/sub]A[sub]2[/sub] = (6; -9; 3), A[sub]1[/sub]A[sub]2[/sub] [$183$] A[sub]3[/sub]A[sub]2[/sub] = 3 [$183$] 6 + (-2) [$183$] (-9) + 3 [$183$] 3 = 18 + 18 + 9 = 45, |A[sub]1[/sub]A[sub]2[/sub]| = |A[sub]2[/sub]A[sub]1[/sub]| = [$8730$]22, |A[sub]3[/sub]A[sub]2[/sub]| = |A[sub]2[/sub]A[sub]3[/sub]| = [$8730$]126. Поэтому и угол между векторами будет иметь ту же величину.
3. Площадь S грани A1A2A3 можно найти по известной из элементарной геометрии формуле для площади треугольника, которая в нашем случае имеет следующий вид: S = 1/2 [$183$] |A[sub]2[/sub]A[sub]1[/sub]| [$183$] |A[sub]2[/sub]A[sub]3[/sub]| [$183$] sin [$966$]. Поскольку
sin [$966$] = [$8730$](1 - cos2 [$966$]) = [$8730$](1 - (45/(2[$8730$]693))2) = [$8730$](1 - 2025/2772) = [$8730$](747/2772) = [$8730$](83/308) [$8776$] 0,5191,
постольку
S = 1/2 [$149$] [$8730$]22 [$183$] [$8730$]126 [$183$] [$8730$](83/308) = [$8730$](57519/308) = [$8730$](747/4) = 3[$8730$]83/2 [$8776$] 13,67.
4. В элементарной геометрии устанавливается, что объём V пирамиды равен 1/3 произведения площади S её основания на высоту h: V = Sh/3. Примем за основание пирамиды её грань A1A2A3 и найдём высоту h. Понятно, что эта высота равна расстоянию между основанием пирамиды и вершиной A4. Найдём расстояние от точки A4 до плоскости A1A2A3.
Специально вводимое понятие векторного произведения векторов как вектора, длина которого равна произведения длин этих векторов на синус угла между ними, а направление определяется исходя из получения правой тройки, образуемых последовательностью направленных отрезков "первый отрезок - второй отрезок - векторное произведение", даёт возможность поступить следующим образом. Найдём векторное произведение векторов A[sub]2[/sub]A[sub]1[/sub] и A[sub]2[/sub]A[sub]3[/sub]:
N = A[sub]2[/sub]A[sub]1[/sub] X A[sub]2[/sub]A[sub]3[/sub] = (-3i + 2j - 3k) X (-6i + 9j - 3k) = 18(i X i) - 27(i X j) + 9(i X k) - 12(j X i) + 18(j X j) - 6(j X k) + 18(k X i) - 27(k X j) + 9(k X k) =
= 0 - 27k - 9j + 12k + 0 - 6i + 18j + 27i + 0 = 21i + 9j - 15k = (21; 9; -15).
Вектор, координаты которого мы установили, направлен перпендикулярно грани A1A2A3, а его длина составляет
|N| = [$8730$]((21)2 + 92 + (-15)2) = [$8730$](441 + 81 + 225) = [$8730$]747 = 3[$8730$]83 [$8776$] 27,33.
Поэтому вектор
n = N/|N| = (21i + 9j - 15k)/(3[$8730$]83) - единичный вектор нормали к плоскости A1A2A3.
Заметим, сравнивая результат вычисления длины векторного произведения с результатом п. 3, что в качестве "бесплатного приложения" мы продемонстрировали альтернативный способ вычисления площади грани A1A2A3: нужно найти векторное произведение векторов, на которых построена грань, и результат разделить пополам.

Отвлечёмся немного и укажем, что если умножить скалярно нормальный вектор плоскости на любой направленный отрезок, расположенный на этой плоскости, то в силу взаимной перпендикулярности сомножителей, получим нуль. Этот способ позволяет найти общее уравнение грани A1A2A3: обозначим через x, y, z координаты произвольной точки M, принадлежащей этой грани; вектор A[sub]1[/sub]M = (x - 2; y + 4; z + 3) расположен на рассматриваемой плоскости; найдём скалярное произведение
(A[sub]2[/sub]A[sub]1[/sub] X A[sub]2[/sub]A[sub]3[/sub]) [$183$] A[sub]1[/sub]M = (21; 9; -15) [$183$] (x - 2; y + 4; z + 3) = 21(x - 2) + 9(y + 4) - 15(z + 3) = 0,
21x + 9y - 15z - 42 + 36 - 45 = 0,
21x + 9y - 15z - 51 = 0 - общее уравнение плоскости A1A2A3.
"Ради интереса" подставим в полученное уравнение координаты точки A2 и проверим, удовлетворяют ли они ему:
21 [$183$] 5 + 9 [$183$] (-6) - 15 [$183$] 0 - 51 = 0,
105 - 54 - 0 - 51 = 0,
0 = 0,
как и должно быть.

Чтобы получить наглядное представление о положении плоскости A1A2A3 в пространстве с введённой на нём декартовой прямоугольной системой координат, выполним следующие тождественные преобразования общего уравнения этой плоскости:
21x + 9y - 15z - 51 = 0,
21x + 9y - 15z = 51,
(21/51)x + (9/51)y - (15/51)z = 1,
x/(51/21) + y/(51/9) + z/(-51/15) = 1,
x/(51/21) + y/(17/3) + z/(-17/5) = 1.
Получили уравнение плоскости A1A2A3 в отрезках на осях координат. Из этого уравнения следует, что рассматриваемая плоскость пересекает ось абсцисс в точке x = 51/21 [$8776$] 2,43, ось ординат - в точке y = 17/3 [$8776$] 5,67, ось аппликат - в точке z = -17/5 = -3,4. Данное обстоятельство может быть использовано при выполнении чертежа пирамиды (но на этом мы останавливаться не будем).
Для "общего развития": поскольку А4(–10;–8; 7), постольку точка А4 расположена в третьем октанте координатного пространства (если непонятно, что это значит, посмотрите здесь). В то же время нормальный вектор плоскости A1A2A3 N = (21; 9; -15) оказывается направленным из начала координат в пятый октант. Можно в качестве нормального вектора плоскости A1A2A3 взять и вектор, направленный противоположно, т. е N' = (-21; -9; 15) (вообще, любой вектор, коллинеарный вектору N, перпендикулярен плоскости A1A2A3). Он "указывает" как раз на третий октант. Единичным вектором соответствующего направления будет тогда вектор n' = (-21i - 9j + 15k)/(3[$8730$]83).
Определим теперь угол, например, между векторами N' и A[sub]1[/sub]A[sub]4[/sub] = (-10 - 2; -8 - (-4); 7 - (-3)) = (-12; -4; 10), имеющим длину
|A[sub]1[/sub]A[sub]4[/sub]| = [$8730$]((-12)2 + (-4)2 + (10)2) = [$8730$](144 + 16 + 100) = [$8730$]260 = 2[$8730$]65.
В результате скалярного умножения получим
N' [$183$] A[sub]1[/sub]A[sub]4[/sub] = (-21; -9; 15) [$183$] (-12; -4; 10) = (-21) [$183$] (-12) + (-9) [$183$] (-4) + 15 [$183$] 10 = 252 + 36 + 150 = 438,
тогда для угла [$968$] между между векторами N' и A[sub]1[/sub]A[sub]4[/sub] найдём
cos [$968$] = 438/(3[$8730$]83 [$183$] 2[$8730$]65) = 438/(6[$8730$]5395) = 219/(3[$8730$]5395) [$8776$] 0,9939,
sin [$968$] = [$8730$](1 - (219/(3[$8730$]5395))2) = [$8730$](1 - 47961/48555) = [$8730$](594/48555) [$8776$] 0,1106.
Понятно, что если вектор A[sub]1[/sub]A[sub]4[/sub] расположен под углом [$968$] к вектору N' - нормальному вектору плоскости A1A2A3, то он расположен под тем же углом и к единичному нормальному вектору n' = (-21i - 9j + 15k)/(3[$8730$]83). Но проекция вектора A[sub]1[/sub]A[sub]4[/sub] на вектор n' является высотой пирамиды, опущенной из вершины A4 на грань A1A2A3. Значит,
h = |A1A4| [$183$] cos [$968$] = 2[$8730$]65 [$183$] 219/(3[$8730$]5395) = 438/(3[$8730$]83) [$8776$] 16,03,
V = Sh/3 = 1/3 [$183$] 3[$8730$]83/2 [$183$] 438/(3[$8730$]83) = 438/6 = 73.
5. Уравнение прямой A1A3, действительно, проще всего получить в виде уравнения прямой, проходящей через две данные точки: A1 и A3. Оно же будет и каноническим уравнением этой прямой. Как было показано в ответе (исправленном) Романа Селивёрстова, получим
(x - 2)/(-3) = (y + 4)/7 = (z + 3)/0.
Выражение (z + 3)/0 не должно Вас смущать. Оно всего лишь отражает то обстоятельство, что прямая A1A3 расположена в плоскости z = -3, откуда
z + 3 = 0. (*)
Далее имеем
(x - 2)/(-3) = (y + 4)/7,
x - 2 = -3(y + 4),
x - 2 = -3y - 12,
x + 3y - 2 + 12 = 0,
x + 3y + 10 = 0. (**)
Система уравнений (*), (**) задаёт прямую A1A3 в общем виде. Уравнение (*) задаёт плоскость, перпендикулярную оси аппликат, а уравнение (**) - плоскость, параллельную этой оси.
Пункты 6, 7, 8 задания рассматривать не будем. Ответы на них могут быть получены рассмотренными выше способами.
Ниже дан чертёж пирамиды.

Если усвоены показанные способы решения, то можно перейти и к использованию матричного исчисления, которое является всего лишь более компактной формой записи этих способов.
С уважением.
Об авторе:
Facta loquuntur.
Facta loquuntur.
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.
