[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-51 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1676.476,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-30T10:51:15.6357483+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6557,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5698},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-29T08:02:54","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-51 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":460.744,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-30T10:51:15.6359262+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5589,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-51 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.329,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-30T10:51:15.6360635+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5274,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-51 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":386.593,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-30T10:51:15.636166+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2447,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-51 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.053,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-30T10:51:15.6362419+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2725,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-51 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.072,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-30T10:51:15.636336+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5715,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-29T10:52:11","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 181742
04.01.2011, 22:07
0.00 руб.
0
5
1
Здравствуйте, уважаемые эксперты! Прошу Вас ответить на следующий вопрос:
1) Найти наибольшие и наименьшие значения функции y=(x+3)/(x^2 + 7) на отрезке [-2;2].
2) Исследовать функцию методом дифференциального исчисления и построить график: y=(1-2x^3)/2x^2.
Спасибо. Оплачено за два вопроса.
1) Найти наибольшие и наименьшие значения функции y=(x+3)/(x^2 + 7) на отрезке [-2;2].
2) Исследовать функцию методом дифференциального исчисления и построить график: y=(1-2x^3)/2x^2.
Спасибо. Оплачено за два вопроса.
Обсуждение

Неизвестный
04.01.2011, 23:21
общий
10.01.2011, 15:10
это ответ
Здравствуйте, Валерия!
1) Чтобы найти наименьшее и наибольшее значения функции на отрезке надо:
а) найти ее значения на концах этого отрезка (т. е. числа y(-2) и y(2)):
y(2) = (2+3)/(2^2+7) = 5/11;
у(-2) = (-2+3)/((-2)^2+7) = 1/11;
б) найти ее значения в точках, где производная функции равна нулю:
y' = [ (x+3)/(x^2+7) ]' = [ (x+3)'(x^2+7) - (x+3)(x^2+7)' ] / (x^2+7)^2 = (-x^2-6x+7)/((x^2+7)^2);
(-x^2-6x+7)/((x^2+7)^2) = 0;
-x^2-6x+7 = 0;
x = -7, x = 1 - точки, в которых производная равна нулю;
x = -7 не принадлежит отрезоку [-2;2]
y(1) = (1+3)/(1^2+7) = 4/8 = 1/2;
в) найти ее значения в точках, где функция не имеет производной;
y' = (-x^2-6x+7)/((x^2+7)^2);
(x^2+7)^2 = 0;
x = ± i√7 (точки не попадают в отрезок, т. к. |x| = √7 = ±2.64)
г) из всех найденных значений выбрать наибольшее и наименьшее:
Наименьшее значение функции y на отрезке [-2;2] min(y) = 1/11;
Наибольшее значение функции у на отрезке [-2;2] max(y) = 1/2.
2) Исследовать функцию методом дифференциального исчисления и построить график: y=(1-2x^3)/2x^2.
Алгоритм исследования функции:
а) найти область определения функции;
б) найти точки пересечения графика функции с осями координат;
в) найти асимптоты;
г) найти точки возможного экстремума;
д) найти критические точки;
е) с помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремумов и точек перегиба;
ж) построить график, учитывая исследование, проведенное в п.а)-е).
а) Область определения функции.
Областью определения функции является множество всех вещественных чисел, кроме x=0;
б) Точки пересечения графика функции с осями координат.
Ох: уравнение 1-2x^3 = 0 имеет один вещественный корень x=1/(2^(1/3)), => точка пересечения с Ох: (1/(2^(1/3)), 0);
Oy: значение уравнения (1-2x^3)/2x^2 при х=0 не определено, поэтому пересечения с осью Оу не будет;
в) Асимптоты:
Исследуем поведение функции вблизи точки разрыва x=0. Так как y → +[$8734$] при х → [$177$]0, то прямая x=0 является вертикальной асимптотой графика функции.
Если х → +∞(x → -∞), то у → 0; следовательно, прямая у=0 является горизонтальной асимптотой графика функции.
y = -x - наклонная асимптота, линия y=kx+b с параметрами
k = limx→∞y(x)/x = limx→∞(1-2x3)/2x3 = -1
b = limx→∞y(x) - k*x = limx→∞1/2x2 = 0
г) Точки возможного экстремума.
Из существования пределов
k = lim [х → +∞(x → -∞)] f(x)/x = lim [х → +∞(x → -∞)] (1-2x^3)/2x^3 = -1;
lim [х → +∞(x → -∞)] (f(x) - kx) = lim [х → +∞(x → -∞)] ((1-2x^3)/2x^2 +x) = 0;
Находим производную и приравниваем к нулю:
y' = [ (1-2x^3)/2x^2 ]' = - (x^3+1)/x^3 = 0;
x^3 = -1,вещественных корней нет, значит, точек возможного экстремума нет (кроме точки х=0).
Вещественный корень один x = -1, y(-1) = 3/2
е) y'(-2) < 0, y'(-1/2) > 0 [$8658$] x = -1 - точка минимума
д) Критические точки.
Для нахождения критических точек вычислим вторую производную:
y'' = (y')' = { [ (1-2x^3)/2x^2 ]' }' = { -(x^3+1)/x^3 }' = {-1- 1/x^3}' = 3/x^4.
Так как y'' в нуль не обращается, то критических точек нет.
Удачи!
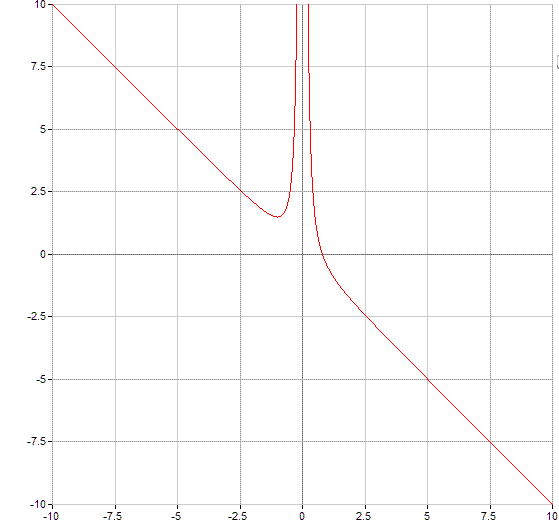
ж) график:
1) Чтобы найти наименьшее и наибольшее значения функции на отрезке надо:
а) найти ее значения на концах этого отрезка (т. е. числа y(-2) и y(2)):
y(2) = (2+3)/(2^2+7) = 5/11;
у(-2) = (-2+3)/((-2)^2+7) = 1/11;
б) найти ее значения в точках, где производная функции равна нулю:
y' = [ (x+3)/(x^2+7) ]' = [ (x+3)'(x^2+7) - (x+3)(x^2+7)' ] / (x^2+7)^2 = (-x^2-6x+7)/((x^2+7)^2);
(-x^2-6x+7)/((x^2+7)^2) = 0;
-x^2-6x+7 = 0;
x = -7, x = 1 - точки, в которых производная равна нулю;
x = -7 не принадлежит отрезоку [-2;2]
y(1) = (1+3)/(1^2+7) = 4/8 = 1/2;
в) найти ее значения в точках, где функция не имеет производной;
y' = (-x^2-6x+7)/((x^2+7)^2);
(x^2+7)^2 = 0;
x = ± i√7 (точки не попадают в отрезок, т. к. |x| = √7 = ±2.64)
г) из всех найденных значений выбрать наибольшее и наименьшее:
Наименьшее значение функции y на отрезке [-2;2] min(y) = 1/11;
Наибольшее значение функции у на отрезке [-2;2] max(y) = 1/2.
2) Исследовать функцию методом дифференциального исчисления и построить график: y=(1-2x^3)/2x^2.
Алгоритм исследования функции:
а) найти область определения функции;
б) найти точки пересечения графика функции с осями координат;
в) найти асимптоты;
г) найти точки возможного экстремума;
д) найти критические точки;
е) с помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремумов и точек перегиба;
ж) построить график, учитывая исследование, проведенное в п.а)-е).
а) Область определения функции.
Областью определения функции является множество всех вещественных чисел, кроме x=0;
б) Точки пересечения графика функции с осями координат.
Ох: уравнение 1-2x^3 = 0 имеет один вещественный корень x=1/(2^(1/3)), => точка пересечения с Ох: (1/(2^(1/3)), 0);
Oy: значение уравнения (1-2x^3)/2x^2 при х=0 не определено, поэтому пересечения с осью Оу не будет;
в) Асимптоты:
Исследуем поведение функции вблизи точки разрыва x=0. Так как y → +[$8734$] при х → [$177$]0, то прямая x=0 является вертикальной асимптотой графика функции.
y = -x - наклонная асимптота, линия y=kx+b с параметрами
k = limx→∞y(x)/x = limx→∞(1-2x3)/2x3 = -1
b = limx→∞y(x) - k*x = limx→∞1/2x2 = 0
г) Точки возможного экстремума.
k = lim [х → +∞(x → -∞)] f(x)/x = lim [х → +∞(x → -∞)] (1-2x^3)/2x^3 = -1;
lim [х → +∞(x → -∞)] (f(x) - kx) = lim [х → +∞(x → -∞)] ((1-2x^3)/2x^2 +x) = 0;
Находим производную и приравниваем к нулю:
y' = [ (1-2x^3)/2x^2 ]' = - (x^3+1)/x^3 = 0;
x^3 = -1,
Вещественный корень один x = -1, y(-1) = 3/2
е) y'(-2) < 0, y'(-1/2) > 0 [$8658$] x = -1 - точка минимума
д) Критические точки.
Для нахождения критических точек вычислим вторую производную:
y'' = (y')' = { [ (1-2x^3)/2x^2 ]' }' = { -(x^3+1)/x^3 }' = {-1- 1/x^3}' = 3/x^4.
Так как y'' в нуль не обращается, то критических точек нет.
Удачи!
ж) график:

Неизвестный
07.01.2011, 01:52
общий
Здравствуйте, Петр!
У Вас много ошибок в ответе.
Здравствуйте, Валерия!
1) Чтобы найти наименьшее и наибольшее значения функции на отрезке надо:
а) найти ее значения на концах этого отрезка (т. е. числа y(-2) и y(2)):
y(2) = (2+3)/(2^2+7) = 5/11;
у(-2) = (-2+3)/((-2)^2+7) = 1/11;
б) найти ее значения в точках, где производная функции равна нулю:
y' = [ (x+3)/(x^2+7) ]' = [ (x+3)'(x^2+7) - (x+3)(x^2+7)' ] / (x^2+7)^2 = (-x^2-6x+7)/((x^2+7)^2);
(-x^2-6x+7)/((x^2+7)^2) = 0;
-x^2-6x+7 = 0;
x = -1, x = 1 - точки, в которых производная равна нулю;
x= -7 , x=1
x= -7 не принадлежит отрезку [-2;2]
y(1) = (1+3)/(1^2+7) = 4/9=4/8=1/2;
y(-1) = (-1+3)/((-1)^2+7) = 2/9=1/4;
в) найти ее значения в точках, где функция не имеет производной;
y' = (-x^2-6x+7)/((x^2+7)^2);
(x^2+7)^2 = 0;
x = ± i√7 (точки не попадают в отрезок, т. к. |x| = √7 = ±2.64)
г) из всех найденных значений выбрать наибольшее и наименьшее:
Наименьшее значение функции y на отрезке [-2;2] min(y) = 1/11;
Наибольшее значение функции у на отрезке [-2;2] max(y) = 5/9=1/2.
2) Исследовать функцию методом дифференциального исчисления и построить график: y=(1-2x^3)/2x^2.
Алгоритм исследования функции:
а) найти область определения функции;
б) найти точки пересечения графика функции с осями координат;
в) найти асимптоты;
г) найти точки возможного экстремума;
д) найти критические точки;
е) с помощью вспомогательного рисунка исследовать знак первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремумов и точек перегиба;
ж) построить график, учитывая исследование, проведенное в п.а)-е).
а) Область определения функции.
Областью определения функции является множество всех вещественных чисел, кроме x=0;
б) Точки пересечения графика функции с осями координат.
Ох: уравнение 1-2x^3 = 0 имеет один вещественный корень x=1/(2^(1/3)), => точка пересечения с Ох: (1/(2^(1/3)), 0);
Oy: значение уравнения (1-2x^3)/2x^2 при х=0 не определено, поэтому пересечения с осью Оу не будет;
в) Асимптоты:
Исследуем поведение функции вблизи точки разрыва x=0. Так как y → 0 при х → -∞, у → +∞ при х → 0, то прямая x=0 является вертикальной асимптотой графика функции.
Если х → +∞(x → -∞), то у → 0; следовательно, прямая у=0 является горизонтальной асимптотой графика функции.
k=limx->[$8734$] y(x)/x=limx->[$8734$] (1/(2*x3)-1)=-1
b=limx->[$8734$] (y(x)-k*x)=limx->[$8734$] (1/(2*x2)-x+x)=0
y= -x - наклонная асимптота
г) Точки возможного экстремума.
Из существования пределов
k = lim [х → +∞(x → -∞)] f(x)/x = lim [х → +∞(x → -∞)] (1-2x^3)/2x^3 = -1;
lim [х → +∞(x → -∞)] (f(x) - kx) = lim [х → +∞(x → -∞)] ((1-2x^3)/2x^2 +x) = 0;
Находим производную и приравниваем к нулю:
y' = [ (1-2x^3)/2x^2 ]' = - (x^3+1)/x^3 = 0;
x^3 = -1, вещественных корней нет, значит, точек возможного экстремума нет (кроме точки х=0).
вещественный корень один: x= -1
д) Критические точки.
Для нахождения критических точек вычислим вторую производную:
y'' = (y')' = { [ (1-2x^3)/2x^2 ]' }' = { -(x^3+1)/x^3 }' = 1/x^3=3/x4.
Так как y'' в нуль не обращается, то критических точек нет.
Вы можете внести исправления в мини-форуме и попросить Администратора Рассылки вставить исправления в ответ.

07.01.2011, 14:42
общий
Да уж, будьте так добры, испавьте.
И предоставьте график. Можете поместить на наш сервер (кнопочка мои файлы) и дать ссылочку

И предоставьте график. Можете поместить на наш сервер (кнопочка мои файлы) и дать ссылочку


Об авторе:
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен

Неизвестный
10.01.2011, 07:03
общий
Хотелось бы поправить и здесь:
в) Асимптоты:
... Так как y → 0 -x при х → +-∞, у → +∞ при х → 0, то прямая x=0 является вертикальной асимптотой графика функции .
Если х → +∞(x → -∞), то у →0; следовательно, прямая у=0 является горизонтальной асимптотой графика функции.
, а прямая y=-x - наклонной асимптотой графика функции.
Непонятно, зачем это:
"Из существования пределов
k = lim [х → +∞(x → -∞)] f(x)/x = lim [х → +∞(x → -∞)] (1-2x^3)/2x^3 = -1;
lim [х → +∞(x → -∞)] (f(x) - kx) = lim [х → +∞(x → -∞)] ((1-2x^3)/2x^2 +x) = 0;"
в) Асимптоты:
... Так как y → 0 -x при х → +-∞, у → +∞ при х → 0, то прямая x=0 является вертикальной асимптотой графика функции .
Если х → +∞(x → -∞), то у →0; следовательно, прямая у=0 является горизонтальной асимптотой графика функции.
, а прямая y=-x - наклонной асимптотой графика функции.
Непонятно, зачем это:
"Из существования пределов
k = lim [х → +∞(x → -∞)] f(x)/x = lim [х → +∞(x → -∞)] (1-2x^3)/2x^3 = -1;
lim [х → +∞(x → -∞)] (f(x) - kx) = lim [х → +∞(x → -∞)] ((1-2x^3)/2x^2 +x) = 0;"

Неизвестный
10.01.2011, 14:45
общий
Адресаты:
На всякий случай, Игорь Витальевич, обращаю Ваше внимание, что пока ещё не поправлена формула в конце:
д) Критические точки.
Для нахождения критических точек вычислим вторую производную:
y'' = (y')' = { [ (1-2x^3)/2x^2 ]' }' = { -(x^3+1)/x^3 }' = {-1- 1/x^3}' = 3/x^4.
Это ничего в выводах не меняет, но все-таки выглядит как ошибка.
И еще я бы выражение
k = limx→∞y(x)/x = limx→∞(1-2x2)/2x2 = -1
b = limx→∞y(x) - k*x = limx→∞1/2x2 = 0
y = -x - наклонная ассимптота
изменил так:
y = -x - наклонная асимптота, линия y=kx+b с параметрами
k = limx→∞ y(x)/x = limx→∞ (1-2x^3)/2x^3 = -1
b = limx→∞ y(x) - k*x = limx→∞ 1/2x^2 = 0
д) Критические точки.
Для нахождения критических точек вычислим вторую производную:
y'' = (y')' = { [ (1-2x^3)/2x^2 ]' }' = { -(x^3+1)/x^3 }' = {-1- 1/x^3}' = 3/x^4.
Это ничего в выводах не меняет, но все-таки выглядит как ошибка.
И еще я бы выражение
k = limx→∞y(x)/x = limx→∞(1-2x2)/2x2 = -1
b = limx→∞y(x) - k*x = limx→∞1/2x2 = 0
y = -x - наклонная ассимптота
изменил так:
y = -x - наклонная асимптота, линия y=kx+b с параметрами
k = limx→∞ y(x)/x = limx→∞ (1-2x^3)/2x^3 = -1
b = limx→∞ y(x) - k*x = limx→∞ 1/2x^2 = 0
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.