[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1679.55,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T19:48:42.8969333+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6545,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-16T11:59:46","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.735,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T19:48:42.8971482+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5577,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.269,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T19:48:42.897267+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5262,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.498,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T19:48:42.897334+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2435,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":223.035,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T19:48:42.8974031+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2713,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.495,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T19:48:42.8975055+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5704,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-11T23:40:15","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 202556
09.04.2022, 15:47
0.00 руб.
09.04.2022, 21:19
0
11
0
Уважаемые эксперты! Пожалуйста, помогите с задачей:
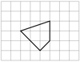
На рисунке показано изображение квадрата в собирающей линзе. Графически или аналитически найдите положение линзы и поясните все сделанные построения и записанные формулы.
Определите фокусное расстояние линзы, если сторона клеточки на рисунке равна 5 см.
Мы не знаем ни положение линзы, ни её оси. Также у изображения 2 стороны перпендикулярны. Помогите, вообще нет идей!

На рисунке показано изображение квадрата в собирающей линзе. Графически или аналитически найдите положение линзы и поясните все сделанные построения и записанные формулы.
Определите фокусное расстояние линзы, если сторона клеточки на рисунке равна 5 см.
Мы не знаем ни положение линзы, ни её оси. Также у изображения 2 стороны перпендикулярны. Помогите, вообще нет идей!
Обсуждение
11.04.2022, 03:15
общий
Адресаты:
У меня нет навыков графического построения в задачах по Оптике. За 70 лет я лишь пару лет назад был вынужден решить свою Оптик-задачу, чтоб узнать Диоптрии в куче своих старых очков и грамотно выбирать очки для наилучшего сохранения остатков моего зрения.
Месяца 3 назад я ещё поизучал оптику, чтоб ответить на пару консультаций (жалко было просителей).
Но Ваша задача - слишком сложна. Я могу попытаться решить её т-ко методом Аналитической геометрии (темы: Прямая на плоскости, Пересечение прямых) с применением формулы линзы и Маткад-помощника. Устроит ли Вас такой вариант? Как Вы будете сдавать преподавателю копии Маткад-формул?
И самое главное: Судя по приложенному Вами чертежу, он по всей вероятности олицетворяет изображение на плоскости, а не проекцию 3х-мерного изображения на плоскость. Уверены ли Вы, что композитор задачи подразумевает, будто изображение плоское?
P.S: Вы писали: "Помогите, вообще нет идей" - "инженерная мысль работает 24 часа в сутки" - и в этой шутке есть большая доля Истины. Я чистил картошку на кухне и мои мысли как-то подсознательно анализировали варианты, как помочь Вам?
Выше-упомянутый метод Аналитической геометрии предполагает составление и решение очень громоздкой системы уравнений для 4х точек Источника, 4х тчк Изображения, координат и формулы линзы, направления оси линзы, уравнений доп-условия перпендикулярности 2х сторон… - более 10 уравнений! Я даже не на 100% уверен, будто Маткад справится с этой громадой.
Но вспомнился совет моего давнего учителя: "Чтоб перехитрить противника, представь себя на его месте". Наш с Вами "условный противник" - изобретатель Ваших заумных задач - будем надеяться, что он вероятно имеет у себя Правильное Решение, то есть он взял координаты чертежа не с потолка, а сделал построение изображения с реального квадрата. Тогда у нас есть зацепка надеяться на успех в упрощённом процессе Решения (такой метод выручал меня на производстве неоднократно).
Суть метода в том, чтобы упростить обрабатываемую фигуру и решать Вашу задачу не для квадрата, а для его части, прямоугольного треугольника (или даже для одной его стороны). Возможно, Вам повезёт, и после Решения треугольника, 4я точка квадрата получится автомати простейшим до-строением ("надурнячка", как говорится). Попробуйте эту идею самостоятельно. Если не одолеете, то "звоните".
Месяца 3 назад я ещё поизучал оптику, чтоб ответить на пару консультаций (жалко было просителей).
Но Ваша задача - слишком сложна. Я могу попытаться решить её т-ко методом Аналитической геометрии (темы: Прямая на плоскости, Пересечение прямых) с применением формулы линзы и Маткад-помощника. Устроит ли Вас такой вариант? Как Вы будете сдавать преподавателю копии Маткад-формул?
И самое главное: Судя по приложенному Вами чертежу, он по всей вероятности олицетворяет изображение на плоскости, а не проекцию 3х-мерного изображения на плоскость. Уверены ли Вы, что композитор задачи подразумевает, будто изображение плоское?
P.S: Вы писали: "Помогите, вообще нет идей" - "инженерная мысль работает 24 часа в сутки" - и в этой шутке есть большая доля Истины. Я чистил картошку на кухне и мои мысли как-то подсознательно анализировали варианты, как помочь Вам?
Выше-упомянутый метод Аналитической геометрии предполагает составление и решение очень громоздкой системы уравнений для 4х точек Источника, 4х тчк Изображения, координат и формулы линзы, направления оси линзы, уравнений доп-условия перпендикулярности 2х сторон… - более 10 уравнений! Я даже не на 100% уверен, будто Маткад справится с этой громадой.
Но вспомнился совет моего давнего учителя: "Чтоб перехитрить противника, представь себя на его месте". Наш с Вами "условный противник" - изобретатель Ваших заумных задач - будем надеяться, что он вероятно имеет у себя Правильное Решение, то есть он взял координаты чертежа не с потолка, а сделал построение изображения с реального квадрата. Тогда у нас есть зацепка надеяться на успех в упрощённом процессе Решения (такой метод выручал меня на производстве неоднократно).
Суть метода в том, чтобы упростить обрабатываемую фигуру и решать Вашу задачу не для квадрата, а для его части, прямоугольного треугольника (или даже для одной его стороны). Возможно, Вам повезёт, и после Решения треугольника, 4я точка квадрата получится автомати простейшим до-строением ("надурнячка", как говорится). Попробуйте эту идею самостоятельно. Если не одолеете, то "звоните".
11.04.2022, 14:25
общий
Адресаты:
Конечно, метод аналитической геометрии только лучше. Лично я пробовал выразить соотношения длин сторон изображения квадрата и связать их с поворотом исходного предмета вокруг главной оптической оси.
11.04.2022, 15:34
общий
Адресаты:
Я не понял Ваше "я пробовал выразить соотношения длин сторон изображения квадрата и связать их с поворотом исходного предмета вокруг главной оптической оси" потому что вращение вокруг оптической оси приводит к 3х-мерному изображению, и оно намного сложнее 2х-мерного, показанного на Вашем чертеже. Может, Вы вращали вокруг центра линзы в пределах плоскости?
Я пока побуду в пассивном ожидании Ваших ответов на ВСЕ мои выше-вопросы.
Я пока побуду в пассивном ожидании Ваших ответов на ВСЕ мои выше-вопросы.
11.04.2022, 15:59
общий
Адресаты:
Можно видеть что главная оптическая ось может быть направлена по разному. Вследствие этого стороны квадрата могут составлять некоторый угол с осью. Но у нас всё происходит только на плоскости.
Я пробовал ввести следующие переменные - фокусное расстояние, расстояние от оптического центра до центра квадрата и угол, который составляют стороны квадрата с главной оптической осью. К сожалению это не увенчались успехом (3 квадратные уравнения). Надеюсь смог объяснить
Я пробовал ввести следующие переменные - фокусное расстояние, расстояние от оптического центра до центра квадрата и угол, который составляют стороны квадрата с главной оптической осью. К сожалению это не увенчались успехом (3 квадратные уравнения). Надеюсь смог объяснить
12.04.2022, 06:32
общий
Адресаты:
Ваша попытка "расстояние от оптического центра до центра квадрата" - ошибочна, тк центр квадрата Вам не даст ничего полезного. Нужно строить по точкам-вершинам. Посмотрите решения похожих задач с построениями треугольника и стрелки:
ПостроениИзображения вЛинзе Ссылка1 \ "Задание EF17760 : Равнобедренный прямоугольный треугольник ABC …"
ГеометричОптика.Задачи+Решения Ссылка2 \ стр=71 : "Построение изображения предмета. Пусть предметом для линзы является стрелка АВ…
На основании построений можно сделать два важных наблюдения: • линза отображает прямую линию в прямую;
• угол между предметом и главной оптической осью отличен от угла между осью и изображением предмета."
"3 квадратные уравнения" - я уже писал Вам : более 10 уравнений! Зачем Вам нужна столь сложная задача? Может быть отменим эту непрактичную затею и переключимся на более простые и полезные задачи?
ПостроениИзображения вЛинзе Ссылка1 \ "Задание EF17760 : Равнобедренный прямоугольный треугольник ABC …"
ГеометричОптика.Задачи+Решения Ссылка2 \ стр=71 : "Построение изображения предмета. Пусть предметом для линзы является стрелка АВ…
На основании построений можно сделать два важных наблюдения: • линза отображает прямую линию в прямую;
• угол между предметом и главной оптической осью отличен от угла между осью и изображением предмета."
"3 квадратные уравнения" - я уже писал Вам : более 10 уравнений! Зачем Вам нужна столь сложная задача? Может быть отменим эту непрактичную затею и переключимся на более простые и полезные задачи?
12.04.2022, 10:15
общий
Адресаты:
Возможно, удобнее делать по-другому, но мне кажется, что уравнения будут симметричнее, если рассматривать следующую картинку. Мы вводим нужные неизвестные, вычисляем координаты точек и находим соответствующие координаты точек-изображений. Дальше находим их отношения (расстояний между точками) и решаем уравнение. Только в ручную это делать слишком трудно...
Прикрепленные файлы:
12.04.2022, 10:22
общий
Адресаты:
Например, координаты самой правой точки квадрата (начало координат - оптический центр линзы)
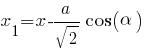 ,
, 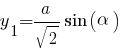
Координаты самой левой точки квадрата:
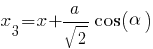 ,
, 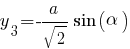
И возможно, решать уравнения с такими "похожими" слагаемыми будет проще.
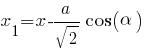 ,
, 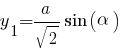
Координаты самой левой точки квадрата:
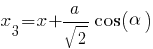 ,
, 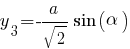
И возможно, решать уравнения с такими "похожими" слагаемыми будет проще.
12.04.2022, 12:05
общий
Адресаты:
Задача очень сложная, решить её сходу и за сегодняшний день не удалось (у нас уже вечер). Поэтому, к концу суток я планирую сделать половину решения, удовлетворяющую частичному Условию. Часа ч-з 4 я покажу его Вам. Заодно я подумаю, как применить Ваше предложение.
P.S: Не удалось решить систему уравнений. Прокрутка Изображения и Исходной фигуры помогла НЕдостаточно. Голова уже болит. Продолжу завтра.
P.S: Не удалось решить систему уравнений. Прокрутка Изображения и Исходной фигуры помогла НЕдостаточно. Голова уже болит. Продолжу завтра.
12.04.2022, 23:59
общий
Адресаты:
Уважаемый автор, полагаю, что прямой угол в фигуре "Изображение" находится на расстоянии d=2F - фокусное расстояние. Точнее, вершина прямого угла находится в двойном фокусе. Далее, надо полагать, что одна из сторон этого самого прямого угла лежит вдоль главной оптической оси, а вторая, соответственно, ей перпендикулярна. Далее, сама плоскость линзы будет Перпендикулярна этой самой главной оптической оси... Т.е., рисунок, который вы исполнили двумя постами выше, где главная опт.ось лежит в горизонте, не может быть хоть сколько нибудь похож на правду.
Об авторе:
С уважением
shvetski
С уважением
shvetski
13.04.2022, 11:12
общий
Адресаты:
Первое впечатление от Вашей задачи - она НЕрешаемая традиционными методами, в которых ГОО (Главная оптическая ось) расположена на оси абсцисс. Ведь если сторона D'C' изображения вертикальна (чертёж прилагаю), тогда и сторона DC оригинала должна быть вертикальной. Но у квадрата-оригинала противоположные стороны - параллельны. Значит, стороны AB и A'B' тоже должны быть вертикальны, что противоречит Условию.
Я больше пол-дня искал в интернете решения задачи, похожей на Вашу, но в огромной куче находок нет построения квадрата ч-з линзу, потому что Ваша задача высокого уровня сложности - она НЕ для школьников и студентов, для её решения надо использовать наклонную ГОО с неизвестным углом наклона. Для этого надо решить громадную систему уравнений с 12 неизвестными (4 пары координат оригинала, 3 параметра Линзы, угол наклона). Это - непосильная задача для моей устаревшей Маткад-версии.
Но что делать, если я нарисовался на странице Вашей Консультации? Всю трудовую жизнь мне поручали технические задачи, которые коллеги считали НЕрешаемыми. А говорить начальнику, что задача невыполнима, мотивирую это своей интуицией, нельзя, тк он сразу заподозрит спеца в некомпетентности, лени… Как получить убедительные факты неоправданной сложности? Надо сделать хоть что-нибудь упрощённо-посильное, временно игнорировать какой-то второстепенный, противоречащий системе параметр.
В Вашей задаче временно игнорируем вершину D', решаем построение для треугольника A'B'C', а в конце, после преодоления главного барьера - упрощённой системы уравнений - проверим, вписывается ли точка D' в Условие?
Я полагаю, Вы уже знаете главную формулу линзы для точки 1/F = 1/d + 1/f , где F - фокусное расстояние, d и f - расстояния от центра линзы до оригинала и изображения.
 Маткад-скриншот с вычислениями и чертежом прилагаю . Я добавил в скрин подробные комментарии зелёным цветом. Как видим, Маткад решил задачу построения треугольника ABC, но 4х-угольник-оригинал ABCD не есть точный квадрат, он искажён на 18% по неравенству сторон квадрата. Для полного, точного решения надо решать гораздо более трудоёмкую задачу с наклонной ГОО.
Маткад-скриншот с вычислениями и чертежом прилагаю . Я добавил в скрин подробные комментарии зелёным цветом. Как видим, Маткад решил задачу построения треугольника ABC, но 4х-угольник-оригинал ABCD не есть точный квадрат, он искажён на 18% по неравенству сторон квадрата. Для полного, точного решения надо решать гораздо более трудоёмкую задачу с наклонной ГОО.
Перед началом любой работы надо оценить её трудоёмкость с целесообразностью. Если на решение упрощённой треуголь-задачи я затратил 2 дня (помимо интернет поисков, за это время я мог бы решить ~ 4 задачи обычной сложности), то решение квадрата потребует обновлять Маткад-версию и возиться ещё 2…3 дня, что не есть разумно, тк эта редкая задача НЕ имеет практической пользы.
Судя по Вашему "вообще нет идей!", Ваш преподаватель ничему не учит Вас, не снабжает ни лекциями, ни методичками, но при этом мучит Вас задачами повышенной сложности. Почему Вы идёте у него на поводу? - я не знаю, это не моё дело. Но если я продолжу помогать Вам, тогда и я буду на поводу у Вашего недобросовестного препода.
Если Вы всё-таки решитесь продолжить уточнённое Решение, тогда я напутствую Вас облегчающим советом: Вместо наклона ГОО гораздо легче использовать наклон исходной картинки вращением изображения вокруг точки A. Вам поможет формула пересчёта исходных координат из системы XOY в систему X'OY' , повёрнутую на угол [$946$] :
x` = x·cos([$946$]) + y·sin([$946$])[$8195$] ,[$8195$] y` = y·cos([$946$]) - x·sin([$946$]) = Удачи!
Я больше пол-дня искал в интернете решения задачи, похожей на Вашу, но в огромной куче находок нет построения квадрата ч-з линзу, потому что Ваша задача высокого уровня сложности - она НЕ для школьников и студентов, для её решения надо использовать наклонную ГОО с неизвестным углом наклона. Для этого надо решить громадную систему уравнений с 12 неизвестными (4 пары координат оригинала, 3 параметра Линзы, угол наклона). Это - непосильная задача для моей устаревшей Маткад-версии.
Но что делать, если я нарисовался на странице Вашей Консультации? Всю трудовую жизнь мне поручали технические задачи, которые коллеги считали НЕрешаемыми. А говорить начальнику, что задача невыполнима, мотивирую это своей интуицией, нельзя, тк он сразу заподозрит спеца в некомпетентности, лени… Как получить убедительные факты неоправданной сложности? Надо сделать хоть что-нибудь упрощённо-посильное, временно игнорировать какой-то второстепенный, противоречащий системе параметр.
В Вашей задаче временно игнорируем вершину D', решаем построение для треугольника A'B'C', а в конце, после преодоления главного барьера - упрощённой системы уравнений - проверим, вписывается ли точка D' в Условие?
Я полагаю, Вы уже знаете главную формулу линзы для точки 1/F = 1/d + 1/f , где F - фокусное расстояние, d и f - расстояния от центра линзы до оригинала и изображения.
Перед началом любой работы надо оценить её трудоёмкость с целесообразностью. Если на решение упрощённой треуголь-задачи я затратил 2 дня (помимо интернет поисков, за это время я мог бы решить ~ 4 задачи обычной сложности), то решение квадрата потребует обновлять Маткад-версию и возиться ещё 2…3 дня, что не есть разумно, тк эта редкая задача НЕ имеет практической пользы.
Судя по Вашему "вообще нет идей!", Ваш преподаватель ничему не учит Вас, не снабжает ни лекциями, ни методичками, но при этом мучит Вас задачами повышенной сложности. Почему Вы идёте у него на поводу? - я не знаю, это не моё дело. Но если я продолжу помогать Вам, тогда и я буду на поводу у Вашего недобросовестного препода.
Если Вы всё-таки решитесь продолжить уточнённое Решение, тогда я напутствую Вас облегчающим советом: Вместо наклона ГОО гораздо легче использовать наклон исходной картинки вращением изображения вокруг точки A. Вам поможет формула пересчёта исходных координат из системы XOY в систему X'OY' , повёрнутую на угол [$946$] :
x` = x·cos([$946$]) + y·sin([$946$])[$8195$] ,[$8195$] y` = y·cos([$946$]) - x·sin([$946$]) = Удачи!

Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.