[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-34 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1679.55,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T14:34:29.6032538+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6545,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-16T11:59:46","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-34 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.735,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T14:34:29.6035043+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5577,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-34 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.269,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T14:34:29.6035968+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5262,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-34 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.498,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T14:34:29.6036617+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2435,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-34 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":223.035,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T14:34:29.6037342+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2713,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-34 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.495,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-18T14:34:29.60385+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5704,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-11T23:40:15","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 201718
20.11.2021, 15:48
0.00 руб.
0
16
1
Здравствуйте! У меня возникли сложности с таким вопросом:
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями где
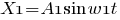
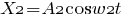
где A1=1 см, А2=1 см w1=0,5 с-1, w2=1 с-1.
Найти уравнение траектории, построить ее с соблюдением масштаба и указать направление движения.
Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями где
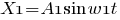
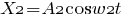
где A1=1 см, А2=1 см w1=0,5 с-1, w2=1 с-1.
Найти уравнение траектории, построить ее с соблюдением масштаба и указать направление движения.
Обсуждение
20.11.2021, 16:38
общий
Адресаты:
Решение похожей задачи см на странице rfpro.ru/question/196606 (Ссылка).
Вам осталось подставить в показанное Решение свои числа.
Вам осталось подставить в показанное Решение свои числа.
20.11.2021, 16:51
общий
 Алексеев Владимир Николаевич
Алексеев Владимир Николаевич Решение похожей задачи см на странице
Я его как раз изучаю. Но что-то у меня график получается сильно вытянутый...
Или я в скобках ошибаюсь в уравнении траектории
21.11.2021, 02:07
общий
Адресаты:
НаЗдоровье Вам! Поздравляю с Успехом! Спасибо Андрею Владимировичу за старания и полноценный Ответ в rfpro.ru/question/196606 !
21.11.2021, 11:49
общий
 Алексеев Владимир Николаевич
Алексеев Владимир Николаевич НаЗдоровье Вам! Поздравляю с Успехом!
 Алексеев Владимир Николаевич
Алексеев Владимир Николаевич Ответ в rfpro.ru/question/196606
Да, основной ход мыслей я взял от туда, но долго не мог понять, почему точки из уравнений условия не попадают на траекторию движения.
Выяснилось, что я не отбросил двойку перед wt в первом уравнении (у меня то ее нет!).
Начал выводить уравнение снова и в итоге получилось уравнение параболы
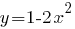 с ветвями вниз.
с ветвями вниз.
21.11.2021, 12:22
общий
Адресаты:
Я очень сомневаюсь в возможности возникновения параболы (линии 2го порядка) из исходных параметрических уравнений первого порядка. Сделайте проверку подставой исходного уравнения
X1 = A1·sin([$969$]1·t) в свою параболу
X1 = A1·sin([$969$]1·t) в свою параболу
21.11.2021, 12:49
общий
 Алексеев Владимир Николаевич
Алексеев Владимир Николаевич X1 = A1·sin(?1·t) в свою параболу
Естественно я проверял, т.к. вычислял направление движения точки. Она начинает движение из 0;1 вправо вниз до точки 1;-1, затем возвращается влево вверх до вершины параболы, далее уходит влево вниз до точки -1;-1.
И точно попадает на траекторию
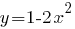
Прикрепленные файлы:
21.11.2021, 12:55
общий
Дано:
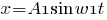
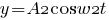
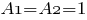 см
см
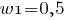
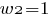
Возведем в квадрат обе части первого уравнения:
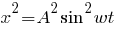
Воспользуемся соотношением:
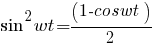
тогда
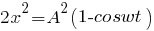
Из второго уравнения системы получаем:
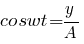
тогда
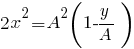
Отсюда получаем уравнение траектории:
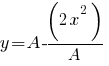
Учитывая A = 1 см, получаем:
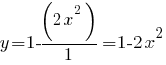
Или что-то не так?
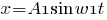
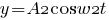
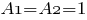 см
см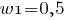
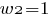
Возведем в квадрат обе части первого уравнения:
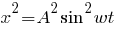
Воспользуемся соотношением:
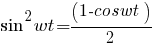
тогда
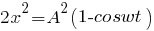
Из второго уравнения системы получаем:
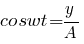
тогда
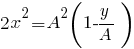
Отсюда получаем уравнение траектории:
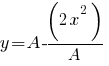
Учитывая A = 1 см, получаем:
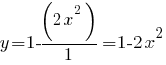
Или что-то не так?
21.11.2021, 14:28
общий
Адресаты:
Чтобы ответственно ответить на Ваш уточняющий вопрос, мне надо вникнуть в Вашу задачу, решить её. Сегодня я сделать это не успеваю, у нас уже поздний вечер по Владивостоку. Продолжу завтра. 

22.11.2021, 05:53
общий
23.11.2021, 03:31
это ответ
Условие: Уравнения колебаний: X1 = A1·sin([$969$]1·t) , X2 = A2·cos([$969$]2·t),
A1 = 1 см, А2 = 1 см, [$969$]1 = 0,5 с-1, [$969$]2 = 1 с-1 .
Вычислить уравнение траектории, построить её с соблюдением масштаба и указать направление движения.
Решение: Заменим временно индекс-содержащие имена переменных на простые и удобные, подставим числовые значения. То есть, максимально упростим формат исходных данных, чтобы не запутаться в процессе решения и не ошибиться. Получаем:
X1(t) = x(t) , X2(t) = y(t) . Тогда уравнения наших колебаний:
x(t) = sin(0,5·t) , y(t) = cos(t) .
Чтобы получить уравнение траектории y(x), надо исключить параметр t из параметрически-заданных уравнений. Для этого воспользуемся тригонометрическими формулами
sin2([$945$]) = [1 - cos(2·[$945$])] / 2 , sin2([$945$]) = 1 - cos2([$945$]) .
В нашей задаче [$945$] = 0,5·t [$8658$] 2·[$945$] = t . Возводим первое уравнение колебания в квадрат:
x(t)2 = sin2([$945$]) = [1 - cos(2·[$945$])] / 2 = [1 - cos(t)] / 2
Из него следует : 2·x(t)2 = 1 - cos(t) [$8658$] cos(t) = 1 - 2·x(t)2
Во втором уравнении y(t) = cos(t) заменяем cos(t) на эквивалент 1 - 2·x(t)2 :
y(t) = 1 - 2·x(t)2 . Теперь можно избавиться от параметра t :
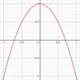
y = 1 - 2·x2 - это Уравнение траектории в удобном для восприятия формате.
Возвращаемся к исходно-заданным именам переменных :
X2(X1) = 1 - 2·X12 - искомое уравнение траектории точки. Строим график:

Вы можете строить график любым удобным Вам способом (в тч используя OnLine-решатели).
Я люблю вычислять в популярном приложении Маткад (ссылка) . Маткад избавляет меня от частых ошибок. Маткад-скриншот с построенным и окультуренным в нём графиком прилагаю. Там же сделана проверка. Я добавил в скрин подробные комментарии зелёным цветом.
Ответ: уравнение траектории : X2(X1) = 1 - 2·X12 .
У этой параболы аргумент изменяется на отрезке X1 = [-1; 1] (тк исходно X1 = sin(…)), множество значений X2 = [-1; 1] .
Направление движения в зависимости от времени я показал стрелочками вдоль кривой траектории.
A1 = 1 см, А2 = 1 см, [$969$]1 = 0,5 с-1, [$969$]2 = 1 с-1 .
Вычислить уравнение траектории, построить её с соблюдением масштаба и указать направление движения.
Решение: Заменим временно индекс-содержащие имена переменных на простые и удобные, подставим числовые значения. То есть, максимально упростим формат исходных данных, чтобы не запутаться в процессе решения и не ошибиться. Получаем:
X1(t) = x(t) , X2(t) = y(t) . Тогда уравнения наших колебаний:
x(t) = sin(0,5·t) , y(t) = cos(t) .
Чтобы получить уравнение траектории y(x), надо исключить параметр t из параметрически-заданных уравнений. Для этого воспользуемся тригонометрическими формулами
sin2([$945$]) = [1 - cos(2·[$945$])] / 2 , sin2([$945$]) = 1 - cos2([$945$]) .
В нашей задаче [$945$] = 0,5·t [$8658$] 2·[$945$] = t . Возводим первое уравнение колебания в квадрат:
x(t)2 = sin2([$945$]) = [1 - cos(2·[$945$])] / 2 = [1 - cos(t)] / 2
Из него следует : 2·x(t)2 = 1 - cos(t) [$8658$] cos(t) = 1 - 2·x(t)2
Во втором уравнении y(t) = cos(t) заменяем cos(t) на эквивалент 1 - 2·x(t)2 :
y(t) = 1 - 2·x(t)2 . Теперь можно избавиться от параметра t :
y = 1 - 2·x2 - это Уравнение траектории в удобном для восприятия формате.
Возвращаемся к исходно-заданным именам переменных :
X2(X1) = 1 - 2·X12 - искомое уравнение траектории точки. Строим график:

Вы можете строить график любым удобным Вам способом (в тч используя OnLine-решатели).
Я люблю вычислять в популярном приложении Маткад (ссылка) . Маткад избавляет меня от частых ошибок. Маткад-скриншот с построенным и окультуренным в нём графиком прилагаю. Там же сделана проверка. Я добавил в скрин подробные комментарии зелёным цветом.
Ответ: уравнение траектории : X2(X1) = 1 - 2·X12 .
У этой параболы аргумент изменяется на отрезке X1 = [-1; 1] (тк исходно X1 = sin(…)), множество значений X2 = [-1; 1] .
Направление движения в зависимости от времени я показал стрелочками вдоль кривой траектории.
5
Спасибо!
22.11.2021, 06:22
общий
Адресаты:
Вы затратили много времени на подробный показ своего неправильного Решения. Гораздо благоразумнее было бы потратить мЕньшее время на простую проверку своего результа. Например, для t = [$960$] = 3,14 сек должно быть:
X1 = sin([$960$]/2) = 1 , X2 = sin([$960$]) = 0 , однако по Вашей формуле
X2([$960$]/2) = 1 - 2·x2 = 1 - 2·sin2([$960$]/2) = 1 - 2·12 = -1 - этот неправильный результ должен побуждать аккуратных людей искать и устранять свою ошибку, а не показывать её подробно на весь СНГ.
Я отправил Вам правильный Ответ, сервер отображает его в начале этой страницы.
X1 = sin([$960$]/2) = 1 , X2 = sin([$960$]) = 0 , однако по Вашей формуле
X2([$960$]/2) = 1 - 2·x2 = 1 - 2·sin2([$960$]/2) = 1 - 2·12 = -1 - этот неправильный результ должен побуждать аккуратных людей искать и устранять свою ошибку, а не показывать её подробно на весь СНГ.
Я отправил Вам правильный Ответ, сервер отображает его в начале этой страницы.
22.11.2021, 09:01
общий
Адресаты:
Добрый день.
Благодарю за Ваше решение. Свой вариант я не в коем случае не декларировал как исключительно верное, однако сбило с толку то, что подстановкой времени (t) в исходные уравнения точка движется прямо по параболе .
.
Вот анимация в онлайн-построителе.
Естественно, я мог в чем-то глубоко заблуждаться.
Благодарю за Ваше решение. Свой вариант я не в коем случае не декларировал как исключительно верное, однако сбило с толку то, что подстановкой времени (t) в исходные уравнения точка движется прямо по параболе
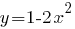 .
.Вот анимация в онлайн-построителе.
Естественно, я мог в чем-то глубоко заблуждаться.
22.11.2021, 11:01
общий
Адресаты:
Наздоровье Вам! Не обижайтесь на старого ворчуна. Я устаю от решений задач. И когда кто-то утверждает, будто он сделал проверку, а ошибка НЕ выявлена, то это раздражает, как обман. Я тоже часто ошибаюсь. И настолько часто, что без Маткада выдаю ошибку на ошибке, что недопустимо для экспертов с высоким статусом. Как Ваш аниматор аккуратно исполнил Вашу ошибку, так и мой Маткад иногда выдаёт абсурды от моих ляп-заданий ему.
Спасибо Вам за аниматор-ссылку!
Спасибо Вам за аниматор-ссылку!

22.11.2021, 21:01
общий
Адресаты:
Да я и не обижаюсь вовсе, просто еще не привык к местным обычаям на данном форуме. Тем более мы земляки-дальневосточники, я сам с Камчатки, служил во Владе и жил там 9 лет на Некрасовской (привет Фрунзенскому району и Первой речке!). Но не суть.
Один из признаков живого ума - это сомневаться в каких-либо решениях, будь то свои или чужие. Верно? Вот смотрите - я не пожалел немного денег и скачал якобы зачтенный вариант этой задачи. Отличие только в том, что x(t) и y(t) объявлены сразу в условии.
Однако, результат решения совпал с моими выкладками. Можете как-то прокомментировать происходящее? Работу с Вашим вариантом я уже отправил на проверку в университет..
Один из признаков живого ума - это сомневаться в каких-либо решениях, будь то свои или чужие. Верно? Вот смотрите - я не пожалел немного денег и скачал якобы зачтенный вариант этой задачи. Отличие только в том, что x(t) и y(t) объявлены сразу в условии.
Однако, результат решения совпал с моими выкладками. Можете как-то прокомментировать происходящее? Работу с Вашим вариантом я уже отправил на проверку в университет..
22.11.2021, 21:07
общий
Адресаты:
И я еще не доглядел - в Вашем решении X2 = A2*sin(wt), а на самом деле в условии X2 = A2*cos(wt)
Похоже, завтра в догонку придется слать письмо преподавателю, дескать, мол ошибся слегка, решал для синуса в x2...
Похоже, завтра в догонку придется слать письмо преподавателю, дескать, мол ошибся слегка, решал для синуса в x2...
23.11.2021, 04:16
общий
Адресаты:
Вы писали : "на самом деле в условии X2 = A2*cos(wt)" - Вы правы, я пол-дня решал для Вас не ту задачу, что Вы указали в Условии, и подвёл Вас на неправильный отчёт преподавателю. Прошу прощения за мой недогляд. 
Я в тот день отправил 3 Ответа - слишком много, хотел побольше помочь людям, но устал и утратил внимательность, хотя всегда стараюсь всё проверить и пере-проверить. Было бы всё нормально, если бы Вы написали Условие текстом полностью, откуда удобно Скопировать/Вставить макси-точно. Но Вы написали своё мат-выражение X2 = A2·cos([$969$]2·t) с использованием тэга "Формула", rfpro.ru-сервер выдал Вашу формулу в формате картинки, и мне пришлось набивать текст вручную. Устаревший движок сервера не поддерживает Юникод с греческими буквами, и поэтому проект Ответа приходится писать в заморочных BBCode , а это такая жопа, что почти все ошибаются. Копию BBCode-текста прилагаю.
Ваш "привет Фрунзенскому району и Первой речке!" передать не могу, тк живу в Облученском р-не фик-Еврейской области (бывший Хабаровский край). У нас т-ко часовой пояс по Владивостоку, а ехать от нас 5 часов до Хабаровска, а потом ещё 12 ч до Владика. Слишком дорого для пенсионеров.
Я исправил свой Ответ. Вы решили свою задачу правильно и раньше меня.

Я в тот день отправил 3 Ответа - слишком много, хотел побольше помочь людям, но устал и утратил внимательность, хотя всегда стараюсь всё проверить и пере-проверить. Было бы всё нормально, если бы Вы написали Условие текстом полностью, откуда удобно Скопировать/Вставить макси-точно. Но Вы написали своё мат-выражение X2 = A2·cos([$969$]2·t) с использованием тэга "Формула", rfpro.ru-сервер выдал Вашу формулу в формате картинки, и мне пришлось набивать текст вручную. Устаревший движок сервера не поддерживает Юникод с греческими буквами, и поэтому проект Ответа приходится писать в заморочных BBCode , а это такая жопа, что почти все ошибаются. Копию BBCode-текста прилагаю.
Ваш "привет Фрунзенскому району и Первой речке!" передать не могу, тк живу в Облученском р-не фик-Еврейской области (бывший Хабаровский край). У нас т-ко часовой пояс по Владивостоку, а ехать от нас 5 часов до Хабаровска, а потом ещё 12 ч до Владика. Слишком дорого для пенсионеров.
Я исправил свой Ответ. Вы решили свою задачу правильно и раньше меня.

Прикрепленные файлы:
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.