[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-37 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1679.293,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T16:37:36.3294131+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6546,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-19T09:51:39","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-37 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.653,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T16:37:36.32962+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5578,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-37 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.191,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T16:37:36.329701+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5263,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-37 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.339,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T16:37:36.3297631+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2436,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-37 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.953,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T16:37:36.3298329+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2714,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-37 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.46,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T16:37:36.3299709+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5705,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-11T23:40:15","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 184516
21.11.2011, 19:00
115.21 руб.
0
12
3
Здравствуйте, уважаемые эксперты! Помогите, пожалуйста, разобраться в решении задачи:
Даны координаты вершины пирамиды ABCD: A(1, -4, 0), B(5, 0, -2), C(3, 7, -10), D (1, -2, 1).
Требуется:
1) записать векторы AB, AC, AD в системе орт и найти модули этих векторов.
2) найти угол между векторами AB, AC
3) найти проекцию вектора AD на вектор AB
4) найти площадь грани АВС
5) найти высоту пирамиды, проведённую из вершины С (2 способа)
6) найти объём пирамиды
7) найти каноническое уравнение прямой, проходящей через точку D перпендикулярно плоскости ABC
8) найти точки пересечения полученной прямой с плоскостью АВС и с координатными плоскостями xOy, xOz, yOz
9) найти уравнение плоскости, проходящей через точку D и C перпендикулярно плоскости АВС.
Можно краткое решение, без подробных комментариев. Думаю, разберусь сам. Для меня главное - формулы, общие методы решения.
В рамках данного вопроса хотелось бы просто уточнить (это из другой задачи, как решать, знаю, но чуть сомневаюсь). Если, например, вектор a=i-5j+2k, это значит, что его координаты (1, -5, 2)?
Даны координаты вершины пирамиды ABCD: A(1, -4, 0), B(5, 0, -2), C(3, 7, -10), D (1, -2, 1).
Требуется:
1) записать векторы AB, AC, AD в системе орт и найти модули этих векторов.
2) найти угол между векторами AB, AC
3) найти проекцию вектора AD на вектор AB
4) найти площадь грани АВС
5) найти высоту пирамиды, проведённую из вершины С (2 способа)
6) найти объём пирамиды
7) найти каноническое уравнение прямой, проходящей через точку D перпендикулярно плоскости ABC
8) найти точки пересечения полученной прямой с плоскостью АВС и с координатными плоскостями xOy, xOz, yOz
9) найти уравнение плоскости, проходящей через точку D и C перпендикулярно плоскости АВС.
Можно краткое решение, без подробных комментариев. Думаю, разберусь сам. Для меня главное - формулы, общие методы решения.
В рамках данного вопроса хотелось бы просто уточнить (это из другой задачи, как решать, знаю, но чуть сомневаюсь). Если, например, вектор a=i-5j+2k, это значит, что его координаты (1, -5, 2)?
Обсуждение

Неизвестный
21.11.2011, 19:42
общий
это ответ
Здравствуйте, Aleksandrkib!
1. АВ=4i+4j-2k
AC=2i+11j-10k
AD=0i+2j+1k
(находятся вычитание из координат конца, координат начала)
lABl=sqrt(16+16+4)=6
lACl=sqrt(4+121+100)=15
lADl=sqrt(0+4+1)=sqrt(5)
(корень из суммы квадратов координат)
sqrt-это обозначение квадратного корня
2. cos(AB^AC)=(x1*x2+y1*y2+z1*z2)/(lABl*lACl)
cos(AB^AC)=(8+44+20)/(6*15)=72/90=8/10
угол AB^AC=arccos(8/10)
3. Проекция находится по формуле lADl*cos(fi), fi-угол между векторами
cos(fi)=(0*4+2*4-2)/(6*sqrt(5))=1/sqrt(5)
Пр.=sqrt(5)*cos(fi)=1
4.S=(ABxAC)/2
то есть нужно найти определитель матрицы
i j k
4 4 -2
2 11 -10
и разделить его на 2
получаем что (-40+22)i-(-40+4)j+(44-8)k=-18i+36j+36k
находим длину вектора sqrt(324+1296+1296)=54
S=54/2=27 кв.ед
1. АВ=4i+4j-2k
AC=2i+11j-10k
AD=0i+2j+1k
(находятся вычитание из координат конца, координат начала)
lABl=sqrt(16+16+4)=6
lACl=sqrt(4+121+100)=15
lADl=sqrt(0+4+1)=sqrt(5)
(корень из суммы квадратов координат)
sqrt-это обозначение квадратного корня
2. cos(AB^AC)=(x1*x2+y1*y2+z1*z2)/(lABl*lACl)
cos(AB^AC)=(8+44+20)/(6*15)=72/90=8/10
угол AB^AC=arccos(8/10)
3. Проекция находится по формуле lADl*cos(fi), fi-угол между векторами
cos(fi)=(0*4+2*4-2)/(6*sqrt(5))=1/sqrt(5)
Пр.=sqrt(5)*cos(fi)=1
4.S=(ABxAC)/2
то есть нужно найти определитель матрицы
i j k
4 4 -2
2 11 -10
и разделить его на 2
получаем что (-40+22)i-(-40+4)j+(44-8)k=-18i+36j+36k
находим длину вектора sqrt(324+1296+1296)=54
S=54/2=27 кв.ед
21.11.2011, 21:10
общий
это ответ
Здравствуйте, Aleksandrkib!
Решение 7 в прикрепленном файле.
Решение 7 в прикрепленном файле.
Прикрепленные файлы:
21.11.2011, 21:29
общий
это ответ
Здравствуйте, Aleksandrkib!
5. Первый способ - воспользоваться известной формулой объёма пирамиды:
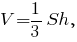
откуда
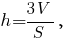
где S - площадь основания пирамиды, на которое опущена высота. В данном случае объём пирамиды уже был найден в задании 6 (18 куб.ед.), площадь же грани ABD можно найти аналогично заданию 4 по формуле:
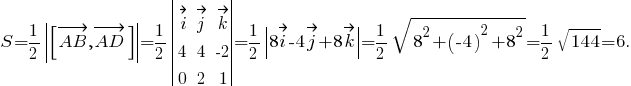
Тогда высота пирамиды составит h = 3·18/6 = 9.
Другой способ - воспользоваться тем, что высота есть кратчайшее расстояние от точки до плоскости основания. Расстояние от точки (x,y,z) до плоскости Ax+By+Cz+D=0 определяется формулой:
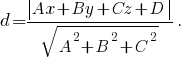
Найдём уравнение плоскости ABD, воспользовавшись тем, что для любой точки M(x, y, z), принадлежащей плоскости, вектора AM, AB и AD будут компланарными (лежать в одной плоскости), то есть их смешанное произведение будет равно 0:
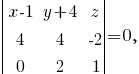
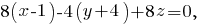
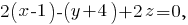
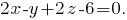
Тогда расстояние от точки C(3,7,-10) до плоскости 2x-y+2z-6=0 будет равно:
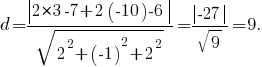
6. Если пирамида построена на трёх векторах a, b, c, имеющих общее начало, то её объём равен
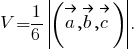
Нам уже известны вектора AB = {4,4,-2}, AC = {2,11,-10} и AD = {0,2,1}, поэтому
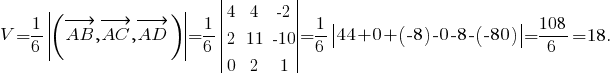
7. Сперва найдём уравнение плоскости ABC. Воспользуемся тем, что для любой точки M(x, y, z), принадлежащей плоскости, вектора AM, AB и AC будут компланарными (лежать в одной плоскости), то есть их смешанное произведение будет равно 0:
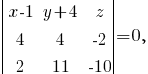
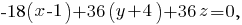
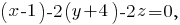
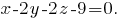
Вектор {1,-2,-2} является нормальным вектором плоскости ABC, следовательно, для прямой, перпендикулярной этой плоскости, он будет направляющим. Учитывая, что она проходит через точку D(1,-2,1), можно записать её каноническое уравнение:
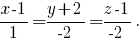
8. Чтобы найти точку пересечения прямой и плоскости, запишем уравнение прямой в параметрическом виде:
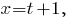
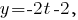
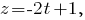
и подставим получившиеся значения в уравнение плоскости. Получим
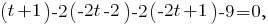
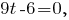
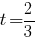
Подставляя в уравнение прямой, получаем x = 5/3, y = -10/3, z = -1/3, то есть точка пересечения прямой и плоскости - (5/3,-10/3,-1/3).
Для точки пересечения с координатной плоскостью xOy, очевидно, z = 0, то есть
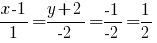
откуда получаем координаты точки пересечения - (3/2,-3,0). Аналогично, для xOz y = 0 и
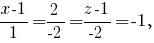
откуда точка пересечения - (0,0,3). Она же, очевидно, является и точкой пересечения с yOz.
9. Если точка M(x, y, z) принадлежит искомой плоскости, то вектора CM, CD и нормальный вектор плоскости ABC (перпендикулярной искомой) будут компланарны, то есть их смешанное произведение будет равно 0 (аналогично заданию 7):
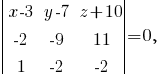
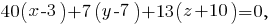
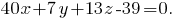
5. Первый способ - воспользоваться известной формулой объёма пирамиды:
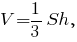
откуда
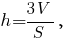
где S - площадь основания пирамиды, на которое опущена высота. В данном случае объём пирамиды уже был найден в задании 6 (18 куб.ед.), площадь же грани ABD можно найти аналогично заданию 4 по формуле:
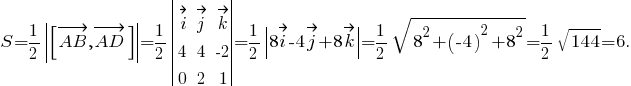
Тогда высота пирамиды составит h = 3·18/6 = 9.
Другой способ - воспользоваться тем, что высота есть кратчайшее расстояние от точки до плоскости основания. Расстояние от точки (x,y,z) до плоскости Ax+By+Cz+D=0 определяется формулой:
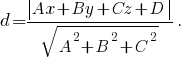
Найдём уравнение плоскости ABD, воспользовавшись тем, что для любой точки M(x, y, z), принадлежащей плоскости, вектора AM, AB и AD будут компланарными (лежать в одной плоскости), то есть их смешанное произведение будет равно 0:
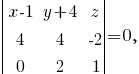
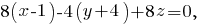
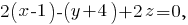
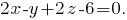
Тогда расстояние от точки C(3,7,-10) до плоскости 2x-y+2z-6=0 будет равно:
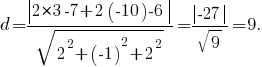
6. Если пирамида построена на трёх векторах a, b, c, имеющих общее начало, то её объём равен
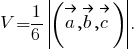
Нам уже известны вектора AB = {4,4,-2}, AC = {2,11,-10} и AD = {0,2,1}, поэтому
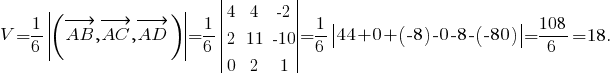
7. Сперва найдём уравнение плоскости ABC. Воспользуемся тем, что для любой точки M(x, y, z), принадлежащей плоскости, вектора AM, AB и AC будут компланарными (лежать в одной плоскости), то есть их смешанное произведение будет равно 0:
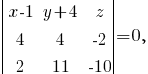
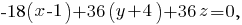
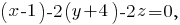
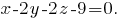
Вектор {1,-2,-2} является нормальным вектором плоскости ABC, следовательно, для прямой, перпендикулярной этой плоскости, он будет направляющим. Учитывая, что она проходит через точку D(1,-2,1), можно записать её каноническое уравнение:
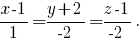
8. Чтобы найти точку пересечения прямой и плоскости, запишем уравнение прямой в параметрическом виде:
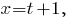
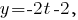
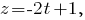
и подставим получившиеся значения в уравнение плоскости. Получим
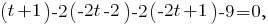
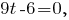
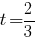
Подставляя в уравнение прямой, получаем x = 5/3, y = -10/3, z = -1/3, то есть точка пересечения прямой и плоскости - (5/3,-10/3,-1/3).
Для точки пересечения с координатной плоскостью xOy, очевидно, z = 0, то есть
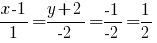
откуда получаем координаты точки пересечения - (3/2,-3,0). Аналогично, для xOz y = 0 и
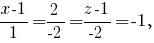
откуда точка пересечения - (0,0,3). Она же, очевидно, является и точкой пересечения с yOz.
9. Если точка M(x, y, z) принадлежит искомой плоскости, то вектора CM, CD и нормальный вектор плоскости ABC (перпендикулярной искомой) будут компланарны, то есть их смешанное произведение будет равно 0 (аналогично заданию 7):
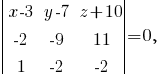
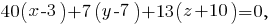
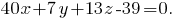
21.11.2011, 21:45
общий
Адресаты:
Здравствуйте, Игорь Витальевич!
На мой взгляд, все девять пунктов задания - неразрывны. То есть эксперт, начавший решение задачи, должен довести его до конца. Решение должно включать ответы на все девять пунктов.
Что по этому поводу думаете Вы?
С уважением.
На мой взгляд, все девять пунктов задания - неразрывны. То есть эксперт, начавший решение задачи, должен довести его до конца. Решение должно включать ответы на все девять пунктов.
Что по этому поводу думаете Вы?
С уважением.
Об авторе:
Facta loquuntur.
Facta loquuntur.
21.11.2011, 21:47
общий
Адресаты:
Если, например, вектор a=i-5j+2k, это значит, что его координаты (1, -5, 2)?
Да.

Об авторе:
Facta loquuntur.
Facta loquuntur.
21.11.2011, 23:17
общий
Адресаты:
все девять пунктов задания - неразрывны
Все-таки, самое главное то, что посетитель получил ответы.
Об авторе:
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
22.11.2011, 07:57
общий
22.11.2011, 08:04
Адресаты:
Уважаемые авторы ответов!
Пользуясь правами модератора портала, обращаю ваше внимание на нежелательность в случаях, подобных данному, "коллективного" подхода к решению задачи. Задание состоит из девяти пунктов, неразрывно связанных между собой. На все девять пунктов задания должен даваться ответ в рамках одного решения. Эксперт, начавший решать задачу, должен довести её решение до конца.
Мы можем обсудить, если кто-то не согласен со мной, ситуацию в отдельной ветке форума портала. Для этого можно оставить сообщение в данном мини-форуме, инициировав такое обсуждение. Но прошу хорошо подумать, прежде чем делать это, чтобы не тратить ваше и моё время попусту.
Кстати, кто из вас берётся продемонстрировать два способа решения в пункте 5 задачи, дополнив свой имеющийся ответ? Появления ещё одного автора ответа в данной консультации я не допущу.
С уважением.
Пользуясь правами модератора портала, обращаю ваше внимание на нежелательность в случаях, подобных данному, "коллективного" подхода к решению задачи. Задание состоит из девяти пунктов, неразрывно связанных между собой. На все девять пунктов задания должен даваться ответ в рамках одного решения. Эксперт, начавший решать задачу, должен довести её решение до конца.
Мы можем обсудить, если кто-то не согласен со мной, ситуацию в отдельной ветке форума портала. Для этого можно оставить сообщение в данном мини-форуме, инициировав такое обсуждение. Но прошу хорошо подумать, прежде чем делать это, чтобы не тратить ваше и моё время попусту.
Кстати, кто из вас берётся продемонстрировать два способа решения в пункте 5 задачи, дополнив свой имеющийся ответ? Появления ещё одного автора ответа в данной консультации я не допущу.
С уважением.

Об авторе:
Facta loquuntur.
Facta loquuntur.
22.11.2011, 14:41
общий
Адресаты:
Могу дополнить свой ответ решением задачи 5 двумя способами и, с вашего позволения, правильным решением задачи 6 (в ответе эксперта Полина, увы, неправильно вычислен определитель, а полученное значение объёма можно использовать в решении задачи 5).
Что касается "коллективного" подхода, он может быть нежелательным только в подобных случаях (когда несколько заданий объединены общими начальными данными, и результат решения одного может быть использован при решении другого). Возможно, эксперту, первым разместившему решение хотя бы части заданий, должно предоставляться преимущественное право и на решение остальных заданий (за этим могут проследить модераторы). Но в интересах автора вопроса не следует делать это ограничение абсолютным: другие эксперты должны иметь право продолжить ответ, если первый эксперт явно сообщит о своём отказе или в случае его долгого (опять-таки, на усмотрение модераторов) молчания.
Что касается "коллективного" подхода, он может быть нежелательным только в подобных случаях (когда несколько заданий объединены общими начальными данными, и результат решения одного может быть использован при решении другого). Возможно, эксперту, первым разместившему решение хотя бы части заданий, должно предоставляться преимущественное право и на решение остальных заданий (за этим могут проследить модераторы). Но в интересах автора вопроса не следует делать это ограничение абсолютным: другие эксперты должны иметь право продолжить ответ, если первый эксперт явно сообщит о своём отказе или в случае его долгого (опять-таки, на усмотрение модераторов) молчания.
22.11.2011, 14:52
общий
Адресаты:
Речь идет именно о подобных случаях.
Никто и не делает ограничение абсолютным. Вы все правильно говорите
Никто и не делает ограничение абсолютным. Вы все правильно говорите

Об авторе:
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
22.11.2011, 14:58
общий
Адресаты:
Что ж, придется ответ Полины удалить...
Об авторе:
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
22.11.2011, 15:58
общий
Адресаты:
Я думаю, что, к сожалению, запрет на коллективное решение подобных задач должен быть абсолютным.

Спасибо Вам, Алексей, за решённый пункт 5.


Об авторе:
Facta loquuntur.
Facta loquuntur.
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.

