[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1679.037,"dynamicRatingStars":9,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T11:58:35.0291192+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6547,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-19T09:51:39","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.57,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T11:58:35.029289+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5579,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.112,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T11:58:35.0293669+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5264,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.18,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T11:58:35.0294271+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2437,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.871,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T11:58:35.0295415+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2715,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-58 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.425,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T11:58:35.0296797+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5705,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-20T13:29:47","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 197278
01.12.2019, 15:35
0.00 руб.
0
6
1
Уважаемые эксперты! Пожалуйста, помогите решить 2 задачи:
Два катера проплыли на расстоянии 15 м друг от друга. Один из них двигался со скоростью 30 км/ч на юго-восток, а другой — со скоростью 40 км/ч на северо-восток. На каком расстоянии друг от друга они окажутся спустя 1,5 часа после встречи, если продолжат движение с постоянными скоростями?
Две моторные лодки отплыли одновременно от одного берега прямолинейного канала с быстрым течением (в момент «старта» они находились совсем рядом). Рулевой первой лодки держал курс строго перпендикулярно берегам, а рулевой второй лодки направлял ее нос под углом 30° к берегу. Лодки двигались с постоянными относительно воды скоростями, и к противоположному берегу причалили одновременно. Ширина канала 70 м. На каком расстоянии друг от друга находились лодки в момент причаливания?
Два катера проплыли на расстоянии 15 м друг от друга. Один из них двигался со скоростью 30 км/ч на юго-восток, а другой — со скоростью 40 км/ч на северо-восток. На каком расстоянии друг от друга они окажутся спустя 1,5 часа после встречи, если продолжат движение с постоянными скоростями?
Две моторные лодки отплыли одновременно от одного берега прямолинейного канала с быстрым течением (в момент «старта» они находились совсем рядом). Рулевой первой лодки держал курс строго перпендикулярно берегам, а рулевой второй лодки направлял ее нос под углом 30° к берегу. Лодки двигались с постоянными относительно воды скоростями, и к противоположному берегу причалили одновременно. Ширина канала 70 м. На каком расстоянии друг от друга находились лодки в момент причаливания?
Обсуждение
05.12.2019, 09:38
общий
это ответ
Здравствуйте, wwesmack! Решаем первую задачу.
Дано : Скорость первого катера V1 = 30 км/час = 8,333 м/с ,
Скорость второго катера V2 = 40 км/час = 11,111 м/с, Дистанция максимального сближения Dm = 15 м.
Вычислить расстояние м-ду катерами спустя [$916$]t = 1,5 часа = 5400 сек.
Решение : Поместим карту движения катеров на координатную плоскость XY так, чтобы ось 0X соответствовала направлению на Восток, а ось 0Y - на Север.
Движение первого катера на юго-восток опишем простейшей системой уравнений :
x1(t) = V1x·t , y1(t) = -V1y·t
Здесь V1x = V1·cos(45°) = 5.893 м/с - проекция скорости первого катера на ось 0X .
V1y = V1·sin(45°) = 5.893 м/с - проекция скорости первого катера на ось 0Y . (V1y = V1x при угле 45°)
Движение второго катера на северо-восток опишем аналогичной системой уравнений :
x2(t) = V2x·t + b , y2(t) = V2y·t + b
Здесь V2x = V2·cos(45°) = 7.857 м/с - проекция скорости второго катера на ось 0X .
V2y = V2·sin(45°) = 7.857 м/с - проекция скорости второго катера на ось 0Y . (V2y = V2x)
b - некоторое смещение катера2 от точки перекрестия траекторий катеров. Если b=0 или отсутствует в уравнениях для обоих катеров, то катера столкнутся в точке перекрестия.
Зависимость дистанции м-ду катерами описывается уравнением
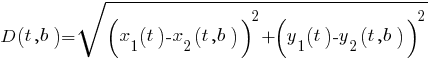
Для вычисления момента встречи t0 надо производную функции D(t,b) приравнять нулю:
dD(t,b)/dt = 0
А чтобы в этот момент встречи катера не столкнулись, а находились на заданном, минимальном расстоянии Dm = 15 м, добавим условие
D(t,b) = Dm
Мы получили систему уравнений:
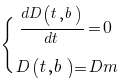
Решать эту систему Вы можете любым удобным для Вас методом. Я решаю в приложении ru.wikipedia.org/wiki/Mathcad . Маткад вычисляет всё быстро и страхует от ошибок типа "человеческий фактор". Маткад-скриншот прилагаю. Я добавил в него подробные комментарии зелёным цветом.

Маткад выдал 2 варианта решения для смещения b второго катера в зависимости от того, который из катеров первым проследует точку встречи так, чтобы не столкнуться и обеспечить мини-дистанцию Dm = 15 м . На графике зависимости дистанции от времени мы с Маткадом показали оба варианта для критического интервала времени вблизи встречи.
После нахождения смещения осталось просто подставить найденные значения времени и смещения в формулу дистанции D(t,b) с добавлением [$916$]t = 5400 сек чтобы получить ответы для 2х вариантов.
Каково же было моё удивление после 2х дней головоломки, когда я увидел ответы, совпавшие в обоих вариантах! Я подумал, что причина совпадения в округлении значений, все-таки 75 км намного больше 15 м!
Я поискал решения похожих задач в интернете - там много решений про встречи катеров и лодок, но такой, как у Вас - с защитным интервалом от столкновения - найти не удалось.
Я задал Маткаду показывть результаты с выводом 14 значащих цифр после запятой (по-умолчанию он выводит на экран 3 знака с округлением последнего, но вычисляет с 15 знаками). Но расхождение было лишь в 11м знаке (в микронах).
Позже до меня дошло, что совпадение получается оттого, что отсчёт ведётся от момента встречи t01 либо t02 (как и задано в Условии задачи!), а НЕ от момента t=0 , когда первый катер прошёл перекрестие траекторий.
Это наводит на подозрение, будто Ваша задача имеет более простое решение, чем проделанное мною.
Но лимит моего времени уже исчерпан.
Ответ : спустя 1,5 часа после встречи расстояние м-ду катерами будет 75 км.
Прилагаю также анимированный график "карты" движения катеров для первого варианта решения (когда катер N1 первым проходит перекрестие тракторий катеров) rfpro.ru/upload/11866
Если Вам ещё нужно решение второй задачи, задайте её в отдельной Консультации (см Правила Портала \ "Как правильно задавать вопросы" rfpro.ru/help/questions#30 "Не задавайте несколько разных вопросов в одном… вероятность того, что Вы получите на них ответы, будет гораздо выше, если Вы зададите их по отдельности… большинство экспертов просто игнорируют вопросы, в которых под видом одного дано несколько вопросов или задач…"
Дано : Скорость первого катера V1 = 30 км/час = 8,333 м/с ,
Скорость второго катера V2 = 40 км/час = 11,111 м/с, Дистанция максимального сближения Dm = 15 м.
Вычислить расстояние м-ду катерами спустя [$916$]t = 1,5 часа = 5400 сек.
Решение : Поместим карту движения катеров на координатную плоскость XY так, чтобы ось 0X соответствовала направлению на Восток, а ось 0Y - на Север.
Движение первого катера на юго-восток опишем простейшей системой уравнений :
x1(t) = V1x·t , y1(t) = -V1y·t
Здесь V1x = V1·cos(45°) = 5.893 м/с - проекция скорости первого катера на ось 0X .
V1y = V1·sin(45°) = 5.893 м/с - проекция скорости первого катера на ось 0Y . (V1y = V1x при угле 45°)
Движение второго катера на северо-восток опишем аналогичной системой уравнений :
x2(t) = V2x·t + b , y2(t) = V2y·t + b
Здесь V2x = V2·cos(45°) = 7.857 м/с - проекция скорости второго катера на ось 0X .
V2y = V2·sin(45°) = 7.857 м/с - проекция скорости второго катера на ось 0Y . (V2y = V2x)
b - некоторое смещение катера2 от точки перекрестия траекторий катеров. Если b=0 или отсутствует в уравнениях для обоих катеров, то катера столкнутся в точке перекрестия.
Зависимость дистанции м-ду катерами описывается уравнением
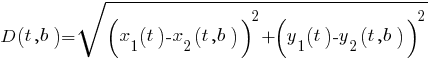
Для вычисления момента встречи t0 надо производную функции D(t,b) приравнять нулю:
dD(t,b)/dt = 0
А чтобы в этот момент встречи катера не столкнулись, а находились на заданном, минимальном расстоянии Dm = 15 м, добавим условие
D(t,b) = Dm
Мы получили систему уравнений:
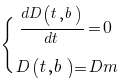
Решать эту систему Вы можете любым удобным для Вас методом. Я решаю в приложении ru.wikipedia.org/wiki/Mathcad . Маткад вычисляет всё быстро и страхует от ошибок типа "человеческий фактор". Маткад-скриншот прилагаю. Я добавил в него подробные комментарии зелёным цветом.

Маткад выдал 2 варианта решения для смещения b второго катера в зависимости от того, который из катеров первым проследует точку встречи так, чтобы не столкнуться и обеспечить мини-дистанцию Dm = 15 м . На графике зависимости дистанции от времени мы с Маткадом показали оба варианта для критического интервала времени вблизи встречи.
После нахождения смещения осталось просто подставить найденные значения времени и смещения в формулу дистанции D(t,b) с добавлением [$916$]t = 5400 сек чтобы получить ответы для 2х вариантов.
Каково же было моё удивление после 2х дней головоломки, когда я увидел ответы, совпавшие в обоих вариантах! Я подумал, что причина совпадения в округлении значений, все-таки 75 км намного больше 15 м!
Я поискал решения похожих задач в интернете - там много решений про встречи катеров и лодок, но такой, как у Вас - с защитным интервалом от столкновения - найти не удалось.
Я задал Маткаду показывть результаты с выводом 14 значащих цифр после запятой (по-умолчанию он выводит на экран 3 знака с округлением последнего, но вычисляет с 15 знаками). Но расхождение было лишь в 11м знаке (в микронах).
Позже до меня дошло, что совпадение получается оттого, что отсчёт ведётся от момента встречи t01 либо t02 (как и задано в Условии задачи!), а НЕ от момента t=0 , когда первый катер прошёл перекрестие траекторий.
Это наводит на подозрение, будто Ваша задача имеет более простое решение, чем проделанное мною.
Но лимит моего времени уже исчерпан.
Ответ : спустя 1,5 часа после встречи расстояние м-ду катерами будет 75 км.
Прилагаю также анимированный график "карты" движения катеров для первого варианта решения (когда катер N1 первым проходит перекрестие тракторий катеров) rfpro.ru/upload/11866
Если Вам ещё нужно решение второй задачи, задайте её в отдельной Консультации (см Правила Портала \ "Как правильно задавать вопросы" rfpro.ru/help/questions#30 "Не задавайте несколько разных вопросов в одном… вероятность того, что Вы получите на них ответы, будет гораздо выше, если Вы зададите их по отдельности… большинство экспертов просто игнорируют вопросы, в которых под видом одного дано несколько вопросов или задач…"
5
06.12.2019, 14:19
общий
Прошу продлить срок жизни этой Консультации на 1 сутки.
Я хочу добавить анимированный график движения катеров, но никогда ранее я не делал такого. Быстро не получается. Надо немного подучиться.
Я хочу добавить анимированный график движения катеров, но никогда ранее я не делал такого. Быстро не получается. Надо немного подучиться.
06.12.2019, 17:47
общий
Или, если совсем уж просто рассуждать, 2 катера движутся по перпендикулярным направлениям со скоростями 30 км/ч и 40 км/ч, поэтому их относительная скорость [$8730$](302+402)=50 км/ч и за 1,5 часа после максимального сближения они разойдутся на 75 км
что до минимального расстояния в 15 метров: имеем 75 км по направлению относительной скорости и 15 м по перпендикуляру к нему - результат практически неотличим от 75 км
что до минимального расстояния в 15 метров: имеем 75 км по направлению относительной скорости и 15 м по перпендикуляру к нему - результат практически неотличим от 75 км
07.12.2019, 11:09
общий
Адресаты:
Вы сразу попали а "десятку" : "если совсем уж просто рассуждать, 2 катера движутся по перпендикулярным направлениям со скоростями 30 км/ч и 40 км/ч, поэтому их относительная скорость [$8730$](302+402)=50 км/ч" - "золотой" прямоугольный треугольник : 32+42=52 ! А я шёл к этому же выводу 2 дня вождения пальцами по стене, имитируя, как это катера должны встречаться, чтоб не столкнуться? Понятно, что перекрестие траекторий они должны проследовать поочерёдно, но не сразу дошло, как это обсчитать?
"Что до минимального расстояния в 15 метров: имеем 75 км по направлению относительной скорости и 15 м по перпендикуляру к нему - результат практически неотличим от 75 км" - а вот и нет! Я пробовал уменьшить время-задержку "спустя 1,5 часа после встречи" до 5 секунд - результ одинаковый для обоих вариантов решения! Потом вообще уменьшил до 0 . Всё равно одинаково! (скриншот прилагаю).
Значит причина не в том, что 75 км "поглощают" 15 м.
У меня уже кораблики бегают по экрану. Спасибо Зенченко Конс Николаичу за сверх-добавленное время. Я ещё повожусь научиться делать паузу в анимации для показа "острых" моментов с выводом на экран их параметров.
"Что до минимального расстояния в 15 метров: имеем 75 км по направлению относительной скорости и 15 м по перпендикуляру к нему - результат практически неотличим от 75 км" - а вот и нет! Я пробовал уменьшить время-задержку "спустя 1,5 часа после встречи" до 5 секунд - результ одинаковый для обоих вариантов решения! Потом вообще уменьшил до 0 . Всё равно одинаково! (скриншот прилагаю).
Значит причина не в том, что 75 км "поглощают" 15 м.
У меня уже кораблики бегают по экрану. Спасибо Зенченко Конс Николаичу за сверх-добавленное время. Я ещё повожусь научиться делать паузу в анимации для показа "острых" моментов с выводом на экран их параметров.
Прикрепленные файлы:
07.12.2019, 12:14
общий
Адресаты:
Если перейти к системе отсчёта, связанной с одной из лодок, то другая движется со скоростью vrel=50 км/ч по прямой, проходящей на расстоянии d=15 м от первой лодки, а время отсчитывается от прохождения точки максимального сближения.
Тогда расстояние d=[$8730$]((vrelt)2+dmin2)
Хотя, уже при t=5 секунд разница между точным значением расстояния и приближением d[$8776$]vrelt составляет всего 1,6 метра.
Так что, при достаточно большой разнице катетов гипотенуза практически не отличается по длине от большего катета
Тогда расстояние d=[$8730$]((vrelt)2+dmin2)
Хотя, уже при t=5 секунд разница между точным значением расстояния и приближением d[$8776$]vrelt составляет всего 1,6 метра.
Так что, при достаточно большой разнице катетов гипотенуза практически не отличается по длине от большего катета
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.