[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1680.063,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-16T17:48:17.9966429+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6543,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-16T11:59:46","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.901,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-16T17:48:17.9968488+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5575,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.426,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-16T17:48:17.9969561+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5260,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.818,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-16T17:48:17.9970206+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2433,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":223.199,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-16T17:48:17.9971556+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2711,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-48 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.566,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-16T17:48:17.9972463+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5702,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-11T23:40:15","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 190909
23.04.2017, 20:48
0.00 руб.
1
2
2
Уважаемые эксперты! Пожалуйста, ответьте на вопрос:
Прикрепленные файлы:
Обсуждение
24.04.2017, 05:48
общий
это ответ
Здравствуйте, soniakechch!
Задача 10.в
Описанная индукция работает только при k >= 2. Очевидно, приведенное рассуждение не позволяет перейти от k = 1 к k = 2.
Задача 10.в
Описанная индукция работает только при k >= 2. Очевидно, приведенное рассуждение не позволяет перейти от k = 1 к k = 2.
24.04.2017, 07:09
общий
это ответ
Здравствуйте, soniakechch!
Рассмотрим задание 10а. При аксиоматическом построении теории натуральных чисел используются аксиомы, одна из которых, называемая аксиомой математической индукции, утверждает следующее: "Пусть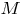 - множество натуральных чисел, обладающее свойствами:
- множество натуральных чисел, обладающее свойствами:
1)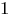 принадлежит
принадлежит 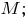
2) если натуральное число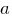 принадлежит
принадлежит 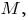 то непосредственно следующее за ним натуральное число
то непосредственно следующее за ним натуральное число  также принадлежит
также принадлежит 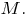
Тогда множество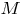 содержит все натуральные числа, то есть
содержит все натуральные числа, то есть 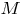 совпадает с
совпадает с  "
"
Из этой аксиомы вытекает законность доказательств методом математической индукции. При этом аксиома математической индукции применяется в следующей форме.
Принцип полной математической индукции. Если некоторое предложение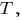 сформулированное для натурального числа
сформулированное для натурального числа 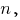 доказано для
доказано для 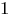 и при допущении его верности для натурального числа
и при допущении его верности для натурального числа 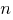 доказана его верность и для следующего натурального числа
доказана его верность и для следующего натурального числа  то предложение
то предложение 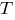 верно для всех натуральных чисел.
верно для всех натуральных чисел.
На принципе полной математической индукции основан метод доказательства теорем, который выглядит так:
Первый шаг. Доказываем верность теоремы для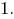
Второй шаг. Допускаем, что теорема верна для натурального числа На основании этого допущения доказываем верность теоремы для
На основании этого допущения доказываем верность теоремы для 
На основании принципа полной математической индукции заключаем, что теорема верна для всякого натурального числа
Воспользуемся этим методом для выполнения задания 10б. При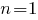 имеем истинное утверждение
имеем истинное утверждение  Предположим, что доказываемое утверждение истинно для некоторого натурального числа
Предположим, что доказываемое утверждение истинно для некоторого натурального числа 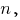 и докажем, что оно истинно для натурального числа
и докажем, что оно истинно для натурального числа  Имеем
Имеем

А это и требовалось доказать. Значит, утверждение

истинно для любого натурального числа
Рассмотрим задание 10а. При аксиоматическом построении теории натуральных чисел используются аксиомы, одна из которых, называемая аксиомой математической индукции, утверждает следующее: "Пусть
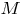 - множество натуральных чисел, обладающее свойствами:
- множество натуральных чисел, обладающее свойствами:1)
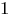 принадлежит
принадлежит 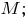
2) если натуральное число
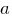 принадлежит
принадлежит 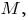 то непосредственно следующее за ним натуральное число
то непосредственно следующее за ним натуральное число  также принадлежит
также принадлежит 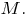
Тогда множество
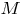 содержит все натуральные числа, то есть
содержит все натуральные числа, то есть 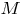 совпадает с
совпадает с  "
"Из этой аксиомы вытекает законность доказательств методом математической индукции. При этом аксиома математической индукции применяется в следующей форме.
Принцип полной математической индукции. Если некоторое предложение
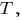 сформулированное для натурального числа
сформулированное для натурального числа 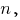 доказано для
доказано для 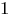 и при допущении его верности для натурального числа
и при допущении его верности для натурального числа 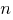 доказана его верность и для следующего натурального числа
доказана его верность и для следующего натурального числа  то предложение
то предложение 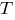 верно для всех натуральных чисел.
верно для всех натуральных чисел.На принципе полной математической индукции основан метод доказательства теорем, который выглядит так:
Первый шаг. Доказываем верность теоремы для
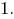
Второй шаг. Допускаем, что теорема верна для натурального числа
 На основании этого допущения доказываем верность теоремы для
На основании этого допущения доказываем верность теоремы для 
На основании принципа полной математической индукции заключаем, что теорема верна для всякого натурального числа

Воспользуемся этим методом для выполнения задания 10б. При
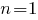 имеем истинное утверждение
имеем истинное утверждение  Предположим, что доказываемое утверждение истинно для некоторого натурального числа
Предположим, что доказываемое утверждение истинно для некоторого натурального числа 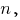 и докажем, что оно истинно для натурального числа
и докажем, что оно истинно для натурального числа  Имеем
Имеем
А это и требовалось доказать. Значит, утверждение

истинно для любого натурального числа

Об авторе:
Facta loquuntur.
Facta loquuntur.
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.


