[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1678.012,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-24T08:30:53.7138637+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6551,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-23T06:46:53","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.239,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-24T08:30:53.7140453+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5583,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":412.798,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-24T08:30:53.7141225+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5267,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":387.543,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-24T08:30:53.7141848+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2441,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-21T19:50:04","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.543,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-24T08:30:53.7142573+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2719,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-30 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.284,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-24T08:30:53.7143425+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5709,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-20T13:29:47","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 190584
21.02.2017, 16:55
0.00 руб.
0
3
2
Здравствуйте! У меня возникли сложности с таким вопросом:
Луч света направлен под прямой x-2y+5=0.Дойдя до прямой 3x-2y+7=0,луч от нее отразился.Составить уравнения прямой,на которой лежит отраженный луч.
Луч света направлен под прямой x-2y+5=0.Дойдя до прямой 3x-2y+7=0,луч от нее отразился.Составить уравнения прямой,на которой лежит отраженный луч.
Обсуждение
22.02.2017, 12:24
общий
это ответ
Здравствуйте, sleepy.zzz!
Я рекомендую Вам выполнить рисунок на бумаге в клетку, чтобы наглядно представить себе ход решения задачи. Ограничусь кратким перечислением этапов возможного варианта решения.
Решая совместно заданные уравнения прямой хода луча и прямой отражения, вычислим координаты точки их пересечения -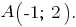
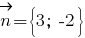- нормальный вектор прямой отражения и направляющий вектор перпендикуляра к этой прямой. Если перпендикуляр проходит через точку 
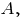то его уравнение можно вывести, используя каноническое уравнение прямой, так:
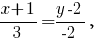
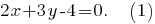
Точка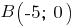
принадлежит прямой хода луча. Если свет падает в направлении, определяемом вектором 
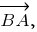то отражаться он будет в направлении, определяемом вектором 
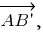где 
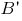- точка, симметричная точке 
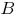относительно перпендикуляра к прямой отражения.
Выведем уравнение прямой, которая проходит через точку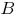 параллельно прямой отражения, учитывая, что направляющим вектором является 
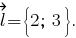Получим
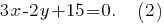
Решая совместно уравнения
вычислим координаты середины отрезка 
- 
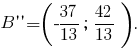
Вычислим координаты точки
Получим
Вычислим координаты вектора
Получим
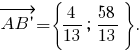
Выведем уравнение искомой прямой. Получим
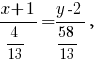
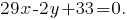
Вам придётся воспроизвести опущенные мной расчёты и проверить правильность результата, используя рисунок, чтобы избежать ошибок.
Я рекомендую Вам выполнить рисунок на бумаге в клетку, чтобы наглядно представить себе ход решения задачи. Ограничусь кратким перечислением этапов возможного варианта решения.
Решая совместно заданные уравнения прямой хода луча и прямой отражения, вычислим координаты точки их пересечения -
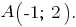
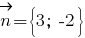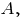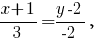
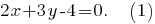
- нормальный вектор прямой отражения и направляющий вектор перпендикуляра к этой прямой. Если перпендикуляр проходит через точку то его уравнение можно вывести, используя каноническое уравнение прямой, так:Точка
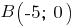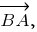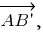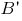принадлежит прямой хода луча. Если свет падает в направлении, определяемом вектором то отражаться он будет в направлении, определяемом вектором где - точка, симметричная точке 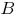относительно перпендикуляра к прямой отражения.Выведем уравнение прямой, которая проходит через точку
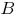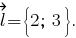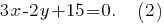
параллельно прямой отражения, учитывая, что направляющим вектором является ПолучимРешая совместно уравнения
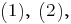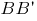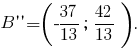
вычислим координаты середины отрезка - Вычислим координаты точки
ПолучимВычислим координаты вектора
Получим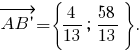Выведем уравнение искомой прямой. Получим
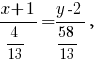
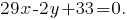
Вам придётся воспроизвести опущенные мной расчёты и проверить правильность результата, используя рисунок, чтобы избежать ошибок.
Об авторе:
Facta loquuntur.
Facta loquuntur.
22.02.2017, 16:29
общий
это ответ
Здравствуйте, sleepy.zzz! Можно еще так. Вторую картинку вставлю в мини форум
Прикрепленные файлы:
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.