[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-08 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1679.165,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T04:08:48.740706+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6546,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-19T09:51:39","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-08 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.611,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T04:08:48.7409026+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5579,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-08 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.151,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T04:08:48.7410108+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5263,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-08 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.259,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T04:08:48.741111+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2436,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-08 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.912,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T04:08:48.7411877+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2715,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-08 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.442,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-20T04:08:48.7412903+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5705,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-20T06:40:09","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 188508
22.12.2015, 17:01
0.00 руб.
0
6
2
Друзья, что-то я с задачкой затупила. Насколько я понимаю это задача на неравенство Чебышева
Вес изделия распределен по нормальному закону. Известно, что абсолютные отклонения веса изделия от его расчетного веса, превосходящие 130 г, встречаются в среднем 31 раз на 1000 изделий. Найти параметр σ распределения веса изделия.




Вес изделия распределен по нормальному закону. Известно, что абсолютные отклонения веса изделия от его расчетного веса, превосходящие 130 г, встречаются в среднем 31 раз на 1000 изделий. Найти параметр σ распределения веса изделия.




Обсуждение
23.12.2015, 09:13
общий
это ответ
Здравствуйте, Елена Васильевна!
Для нормально распределенной случайной величины X со средним значением [$956$]:
P(|X - [$956$]|<a) = erf(a/([$963$][$8730$]2).
По условию задачи для a = 130 г эта вероятность равна 1 - 31/1000 = 0.969.
Уравнение
erf(x) = 0.969
имеет решение x = 1.52528. Его можно найти по таблицам, используюя линейную интерполяцию, или с помощью какой-либо из доступных математических программ. В результате имеем:
130/([$963$][$8730$]2) = 1.52528,
откуда получим искомое среднеквадратичное отклонение:
[$963$] = 130/(1.52528[$8730$]2) = 60.26
P.S. Неравенство Чебышёва дает оценку снизу на величину [$963$] для любого (не только нормального) распределения:
P(|X - [$956$]|[$8805$]a) [$8804$] [$963$]2/a2
Из условий задачи находим:
(31/1000)*1302 [$8804$] [$963$]2,
[$963$] [$8805$] 22.89.
Для нормально распределенной случайной величины X со средним значением [$956$]:
P(|X - [$956$]|<a) = erf(a/([$963$][$8730$]2).
По условию задачи для a = 130 г эта вероятность равна 1 - 31/1000 = 0.969.
Уравнение
erf(x) = 0.969
имеет решение x = 1.52528. Его можно найти по таблицам, используюя линейную интерполяцию, или с помощью какой-либо из доступных математических программ. В результате имеем:
130/([$963$][$8730$]2) = 1.52528,
откуда получим искомое среднеквадратичное отклонение:
[$963$] = 130/(1.52528[$8730$]2) = 60.26
P.S. Неравенство Чебышёва дает оценку снизу на величину [$963$] для любого (не только нормального) распределения:
P(|X - [$956$]|[$8805$]a) [$8804$] [$963$]2/a2
Из условий задачи находим:
(31/1000)*1302 [$8804$] [$963$]2,
[$963$] [$8805$] 22.89.
5
23.12.2015, 09:33
общий
Адресаты:
Как я понимаю, задачу можно решить следующим образом.
Согласно неравенству Чебышёва, вероятность того, что отклонение случайной величины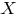 от её математического ожидания по абсолютной величине меньше положительного числа
от её математического ожидания по абсолютной величине меньше положительного числа 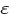 , не меньше, чем
, не меньше, чем 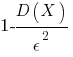 :
:
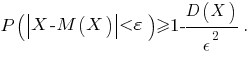
Можно показать, что для противоположного события
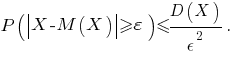
В рассматриваемой задаче в соответствии с последним неравенством имеем
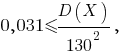
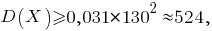
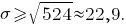
Согласно неравенству Чебышёва, вероятность того, что отклонение случайной величины
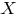 от её математического ожидания по абсолютной величине меньше положительного числа
от её математического ожидания по абсолютной величине меньше положительного числа 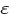 , не меньше, чем
, не меньше, чем 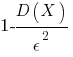 :
: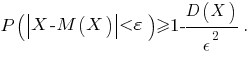
Можно показать, что для противоположного события
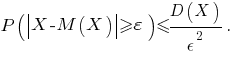
В рассматриваемой задаче в соответствии с последним неравенством имеем
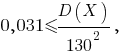
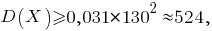
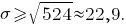
Об авторе:
Facta loquuntur.
Facta loquuntur.
23.12.2015, 09:34
общий
это ответ
Здравствуйте, Елена Васильевна!
Как я понимаю, задачу можно решить следующим образом.
Согласно неравенству Чебышёва, вероятность того, что отклонение случайной величины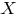 от её математического ожидания по абсолютной величине меньше положительного числа
от её математического ожидания по абсолютной величине меньше положительного числа 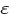 , не меньше, чем
, не меньше, чем 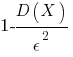 :
:
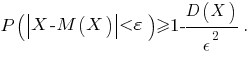
Можно показать, что для противоположного события
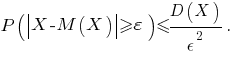
В рассматриваемой задаче в соответствии с последним неравенством имеем
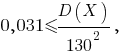
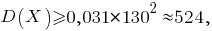
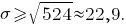
С уважением.
Как я понимаю, задачу можно решить следующим образом.
Согласно неравенству Чебышёва, вероятность того, что отклонение случайной величины
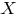 от её математического ожидания по абсолютной величине меньше положительного числа
от её математического ожидания по абсолютной величине меньше положительного числа 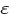 , не меньше, чем
, не меньше, чем 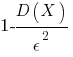 :
: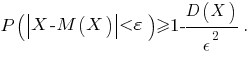
Можно показать, что для противоположного события
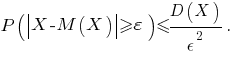
В рассматриваемой задаче в соответствии с последним неравенством имеем
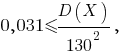
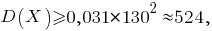
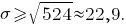
С уважением.
5
Спасибо
Об авторе:
Facta loquuntur.
Facta loquuntur.
23.12.2015, 09:41
общий
Спасибо за помощь. Только начинаю разбираться в теории вероятности. В Вузе можно сказать этот раздел математики пролентяйничала. Вот теперь занимаюсь самообразованием. Но такие задачи еще сложны для меня.
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.


