[{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-26 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"Facta loquuntur.","signatureHTML":"Facta loquuntur.","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.979,"absoluteRating":109927,"dynamicRating":1679.293,"dynamicRatingStars":10,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T14:26:58.1896915+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":6546,"questions":12,"questionsPosts":18345,"questionsAnswers":6663,"questionsPostsEvaluations":2831,"forumPosts":5697},"isRfproUserClass":true,"id":17387,"name":"Гордиенко Андрей Владимирович","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-19T09:51:39","photo":"users/17387/f4979bc95a484b9f43f75cfe66538acd.jpg","lastDateIndicatorClass":"red","lastDateIndicatorText":"давно","photoPreview200":"users/17387/200_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview120":"users/17387/120_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview100":"users/17387/100_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview80":"users/17387/80_f4979bc95a484b9f43f75cfe66538acd.jpg","photoPreview40":"users/17387/40_f4979bc95a484b9f43f75cfe66538acd.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-26 мин."},"isBanned":false,"roleString":"Мастер-Эксперт","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\nЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","aboutHTML":"Я пенсионер. Образование высш, радио-инж. Работал инж-электроником, ведущим средств телевидения, связи, слесарем и инженером КИП, грузчиком, программистом. На моём счету десятки рац-предложений, в тч с большим экономич эффектом.\u003Cbr\u003EЯ люблю компьютеры, ремонтирую их друзьям и соседям. Пишу полезные программки в vbs-файлах, автоматизирующие настройку Win-систем, приложений и работу с ними.","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.935,"absoluteRating":25753,"dynamicRating":461.653,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T14:26:58.1898772+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":11,"counters":{"daysAtPortal":5578,"questions":25,"questionsPosts":7459,"questionsAnswers":1225,"questionsPostsEvaluations":788,"forumPosts":399},"isRfproUserClass":true,"id":259041,"name":"Алексеев Владимир Николаевич","email":"","role":10,"registDate":"1000-01-01T00:00:00","lastDate":"2024-01-30T15:24:45","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-26 мин."},"isBanned":false,"roleString":"Старший Модератор","roleIcon":"fa-user-tie","socialMedia":[],"aboutText":"634034, г.Томск, ул.Красноармейская 122, кв.173","aboutHTML":"634034, г.Томск, ул.Красноармейская 122, кв.173","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.985,"absoluteRating":21746,"dynamicRating":413.191,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T14:26:58.1900036+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":13,"counters":{"daysAtPortal":5263,"questions":1,"questionsPosts":1973,"questionsAnswers":1283,"questionsPostsEvaluations":588,"forumPosts":91},"isRfproUserClass":true,"id":312929,"name":"Коцюрбенко Алексей Владимирович","email":"","role":12,"registDate":"1000-01-01T00:00:00","lastDate":"2023-11-05T17:20:40","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-26 мин."},"isBanned":false,"roleString":"Советник","roleIcon":"fa-user-ninja","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":5,"absoluteRating":9460,"dynamicRating":388.339,"dynamicRatingStars":8,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T14:26:58.1900768+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":10,"counters":{"daysAtPortal":2436,"questions":0,"questionsPosts":472,"questionsAnswers":398,"questionsPostsEvaluations":298,"forumPosts":1},"isRfproUserClass":true,"id":401284,"name":"Михаил Александров","email":"","role":9,"registDate":"1000-01-01T00:00:00","lastDate":"2024-03-27T19:23:59","photo":"users/401284/48171011af39b6bb3a74df8c0fcf97d0.jpg","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"users/401284/200_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview120":"users/401284/120_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview100":"users/401284/100_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview80":"users/401284/80_48171011af39b6bb3a74df8c0fcf97d0.jpg","photoPreview40":"users/401284/40_48171011af39b6bb3a74df8c0fcf97d0.jpg","isPhotoExists":true,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":true},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-26 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"","signatureHTML":"","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.987,"absoluteRating":6052,"dynamicRating":222.953,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T14:26:58.1901513+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":2714,"questions":0,"questionsPosts":527,"questionsAnswers":250,"questionsPostsEvaluations":155,"forumPosts":0},"isRfproUserClass":true,"id":400669,"name":"epimkin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-02-19T23:46:05","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false},{"isEmailConfirmed":true,"tel":"","ip":"0.0.0.0","ipLocation":{"ip":"","sDate":3,"postalCode":"","country":"","countryIsoCode":"","federalDistrict":"","region":"","regionType":"","city":"","cityType":"","geoLat":"","geoLon":"","locationString":""},"birthDate":"0001-01-01T00:00:00","age":0,"isBirthdayToday":false,"ban":{"id":0,"userId":0,"isBanned":false,"startDate":"0001-01-01T00:00:00","endDate":"0001-01-01T00:00:00","moder":{"id":0,"name":"Неизвестный","email":"нет адреса","role":0,"roleString":"Неподтвержден","roleIcon":"fa-user-clock","registDate":"0001-01-01T00:00:00","lastDate":"0001-01-01T00:00:00","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isValid":false,"isLoggedIn":false,"isUnconfirmed":true,"isConfirmed":false,"isNewUser":false,"isExisted":false,"isExpert":false,"isRfproUserClass":false},"reasonHTML":"","timeToUnbanString":"-26 мин."},"isBanned":false,"roleString":"Посетитель","roleIcon":"fa-user","socialMedia":[],"aboutText":"","aboutHTML":"","signatureText":"[i]С уважением[/i]\n[i]shvetski[/i]","signatureHTML":"\u003Ci\u003EС уважением\u003C/i\u003E\u003Cbr\u003E\u003Ci\u003Eshvetski\u003C/i\u003E","country":{"id":0,"name":"","isFlagExists":false,"flagImage":"","isValid":false},"city":{"id":0,"name":"","countryId":0,"yandexCityId":0,"isValid":false},"averageEvaluation":4.963,"absoluteRating":11493,"dynamicRating":201.46,"dynamicRatingStars":7,"timezone":{"id":0,"baseUtcOffset":"00:00:00","displayName":"[не установлен]","linuxid":"notset/clean"},"currentDateTime":"2024-04-19T14:26:58.1902699+03:00","isValid":true,"isUnconfirmed":false,"isConfirmed":true,"settings":{"fixedHeader":true,"fixedFooter":true,"leftColumnMode":2,"darkTheme":false,"topPanelBtns":[{"id":103,"text":"Главная","title":"Главная (начальная) страница Портала","icon":"fa-solid fa-house-chimney","colorClass":"text-info-emphasis","controller":"Home","action":"Index","accessLevel":0,"isDropdown":false},{"id":100,"text":"Вход в систему","title":"Войти в систему с использованием своих регистрационных данных (адрес электронной почты и пароль)","icon":"fa-solid fa-arrow-right-to-bracket","colorClass":"text-info-emphasis","controller":"Login","action":"Index","accessLevel":0,"isDropdown":false},{"id":101,"text":"Регистрация","title":"Зарегистрироваться в системе и стать полноценным участником сообщества","icon":"fa-solid fa-user-plus","colorClass":"text-info-emphasis","controller":"Regist","action":"Index","accessLevel":0,"isDropdown":false},{"id":102,"text":"Сброс пароля","title":"Сбросить пароль свой учетной записи, если Вы его забыли","icon":"fa-solid fa-key","colorClass":"text-danger-emphasis","controller":"Login","action":"ResetPassword","accessLevel":0,"isDropdown":false}],"topPanelBtnsHideText":false},"isLevelUpAllowed":false,"nextRole":2,"counters":{"daysAtPortal":5705,"questions":35,"questionsPosts":1567,"questionsAnswers":588,"questionsPostsEvaluations":324,"forumPosts":44},"isRfproUserClass":true,"id":226425,"name":"Konstantin","email":"","role":1,"registDate":"1000-01-01T00:00:00","lastDate":"2024-04-11T23:40:15","photo":"images/unophoto.png?v=9.4.12","lastDateIndicatorClass":"gray","lastDateIndicatorText":"давно","photoPreview200":"images/unophoto.png?v=9.4.12","photoPreview120":"images/unophoto.png?v=9.4.12","photoPreview100":"images/unophoto.png?v=9.4.12","photoPreview80":"images/unophoto.png?v=9.4.12","photoPreview40":"images/unophoto.png?v=9.4.12","isPhotoExists":false,"isLoggedIn":true,"isNewUser":false,"isExisted":true,"isExpert":false}]
Консультация № 188333
05.12.2015, 20:25
0.00 руб.
0
16
1
Уважаемые эксперты!
Задача такая: точка, двигаясь по поверхности шара радиуса R, описывает окружности равного диаметра в проекции на каждой из трех координатных плоскостей.
Необходимо вывести уравнение траектории движения точки.
С наилучшими пожеланиями,
Георгий Шишков
Задача такая: точка, двигаясь по поверхности шара радиуса R, описывает окружности равного диаметра в проекции на каждой из трех координатных плоскостей.
Необходимо вывести уравнение траектории движения точки.
С наилучшими пожеланиями,
Георгий Шишков
Обсуждение
06.12.2015, 10:00
общий
Адресаты:
Интересно, из какого источника эта задача?
Первое, что представляется, это система трёх уравнений и одного неравенства. Если поместить начало декартовой прямоугольной системы координат в центр шара, то r[$8804$]R, x[sup]2[/sup]+y[sup]2[/sup]=r[sup]2[/sup], y[sup]2[/sup]+z[sup]2[/sup]=r[sup]2[/sup], z[sup]2[/sup]+x[sup]2[/sup]=r[sup]2[/sup].
Первое, что представляется, это система трёх уравнений и одного неравенства. Если поместить начало декартовой прямоугольной системы координат в центр шара, то r[$8804$]R, x[sup]2[/sup]+y[sup]2[/sup]=r[sup]2[/sup], y[sup]2[/sup]+z[sup]2[/sup]=r[sup]2[/sup], z[sup]2[/sup]+x[sup]2[/sup]=r[sup]2[/sup].
Об авторе:
Facta loquuntur.
Facta loquuntur.
06.12.2015, 14:58
общий
Адресаты:
Но представить себе такую траекторию я не могу. 

Об авторе:
Facta loquuntur.
Facta loquuntur.
07.12.2015, 09:38
общий
Уважаемый Andy,
Попытка решения этой задачи - проверка на "вшивость" одной умозрительной альтернативной физической теории. Есть предположение, в частности, что витание частиц в броуновском движении, происходит не хаотически-статистически, а по таким траекториям.
Траектория может быть похожа на логотип компании Adobe.
С наилучшими пожеланиями,
Георгий Шишков
Попытка решения этой задачи - проверка на "вшивость" одной умозрительной альтернативной физической теории. Есть предположение, в частности, что витание частиц в броуновском движении, происходит не хаотически-статистически, а по таким траекториям.
Траектория может быть похожа на логотип компании Adobe.
С наилучшими пожеланиями,
Георгий Шишков
07.12.2015, 10:03
общий
Адресаты:
Разве логотип компании "Adobe" имеет что-то общее с кривыми, расположенными на сфере?
Об авторе:
Facta loquuntur.
Facta loquuntur.
07.12.2015, 16:25
общий
07.12.2015, 16:34
Адресаты:
По-видимому, нет оснований предполагать, что центры проекций искомой траектории на координатные плоскости совпадают с проекциями центра шара. Тогда, разумеется, уравнения, написанные мной в первом сообщении, неправильные.
Кроме того, окружности одинакового диаметра полностью определяют проекции траектории на координатные плоскости или только являются их частями? Если имеется в виду последнее, то можно представить себе петлевидную траекторию, состоящую из трёх окружностей, касающихся друг друга.
Кроме того, окружности одинакового диаметра полностью определяют проекции траектории на координатные плоскости или только являются их частями? Если имеется в виду последнее, то можно представить себе петлевидную траекторию, состоящую из трёх окружностей, касающихся друг друга.

Об авторе:
Facta loquuntur.
Facta loquuntur.
08.12.2015, 00:17
общий
Уважаемый Andy,
В приложенном файле, предполагаемый вид траектории.
Всего доброго,
Георгий Шишков
В приложенном файле, предполагаемый вид траектории.
Всего доброго,
Георгий Шишков
Прикрепленные файлы:
08.12.2015, 06:23
общий
Адресаты:
Как я вижу, проекциями такой фигуры на три взаимно перпендикулярные плоскости не будут три окружности.
Об авторе:
Facta loquuntur.
Facta loquuntur.
08.12.2015, 07:27
общий
Уважаемый Andy,
На рисунке - принцип. Аксонометрию с окружностями в проекциях, привести не смог.
Всего доброго,
Георгий Шишков
На рисунке - принцип. Аксонометрию с окружностями в проекциях, привести не смог.
Всего доброго,
Георгий Шишков
08.12.2015, 08:29
общий
Адресаты:
По-моему, можно представить траекторию, состоящую из окружностей одинакового диаметра, оси которых взаимно перпендикулярны, а сами окружности касаются друг друга. Однако, проекции такой траектории будут состоять не только из окружностей, но и из отрезков прямых. Вас это устроит?
Срок действия консультации я продлил на 5 суток.
Срок действия консультации я продлил на 5 суток.
Об авторе:
Facta loquuntur.
Facta loquuntur.
09.12.2015, 00:04
общий
Уважаемый Andy,
Да, устроит. Траектория ведь будет гладкой кривой! Насколько я понимаю, Вы возвращаетесь к первоначальной системе уравнений + неравенство?
Всего доброго,
Георгий Шишков
Да, устроит. Траектория ведь будет гладкой кривой! Насколько я понимаю, Вы возвращаетесь к первоначальной системе уравнений + неравенство?
Всего доброго,
Георгий Шишков
09.12.2015, 06:37
общий
Адресаты:
Да, возвращаюсь. Но неравенство не нужно. По-моему, радиусы окружностей равны половинам сторон куба, вписанного в шар. Диагональ такого куба равна диаметру шара.
С другой стороны, детальное описание проекций требует описания не только окружностей, проецируемых в натуральную величину, но и отрезков, являющихся проекциями других участков траектории на каждую из плоскостей проекций. Иначе сама траектория не будет определена однозначно. Вы понимаете, что я имею в виду?
С другой стороны, детальное описание проекций требует описания не только окружностей, проецируемых в натуральную величину, но и отрезков, являющихся проекциями других участков траектории на каждую из плоскостей проекций. Иначе сама траектория не будет определена однозначно. Вы понимаете, что я имею в виду?
Об авторе:
Facta loquuntur.
Facta loquuntur.
09.12.2015, 15:16
общий
10.12.2015, 06:50
Адресаты:
Как мне представляется, траектория состоит из трёх окружностей, оси которых попарно взаимно перпендикулярны. Выберем начало O декартовой прямоугольной системы координат в центре шара. Пусть первая окружность проецируется в натуральную величину на плоскость Oxy, вторая - на плоскость Oyz, третья - на плоскость Oxz.
Запишем уравнение поверхности шара:
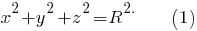
Первая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oxy на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.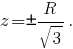
Вторая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oyz на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.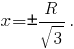
Третья окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Ozx на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.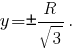
Каждая из окружностей, проецируясь одинаковым образом, может быть расположена в пространстве одним из двух способов. Например, первая окружность может быть расположена или в плоскости верхней, или в плоскости нижней грани куба, вписанного в поверхность шара, если полагать плоскость Oxy расположенной горизонтально. Соответственно выбирается тот или иной знак во втором уравнении каждой из трёх систем.
Можно ли из этих систем уравнений получить уравнение траектории в виде одной формулы, я не знаю.
Запишем уравнение поверхности шара:
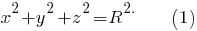
Первая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oxy на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.
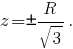
Вторая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oyz на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.
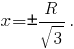
Третья окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Ozx на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.
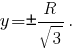
Каждая из окружностей, проецируясь одинаковым образом, может быть расположена в пространстве одним из двух способов. Например, первая окружность может быть расположена или в плоскости верхней, или в плоскости нижней грани куба, вписанного в поверхность шара, если полагать плоскость Oxy расположенной горизонтально. Соответственно выбирается тот или иной знак во втором уравнении каждой из трёх систем.
Можно ли из этих систем уравнений получить уравнение траектории в виде одной формулы, я не знаю.
Об авторе:
Facta loquuntur.
Facta loquuntur.
10.12.2015, 06:51
общий
это ответ
Здравствуйте, georgy_shishkov!
Как мне представляется, траектория состоит из трёх окружностей, оси которых попарно взаимно перпендикулярны. Выберем начало O декартовой прямоугольной системы координат в центре шара. Пусть первая окружность проецируется в натуральную величину на плоскость Oxy, вторая - на плоскость Oyz, третья - на плоскость Oxz.
Запишем уравнение поверхности шара:
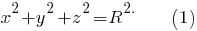
Первая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oxy на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.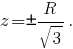
Вторая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oyz на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.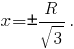
Третья окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Ozx на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.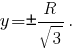
Каждая из окружностей, проецируясь одинаковым образом, может быть расположена в пространстве одним из двух способов. Например, первая окружность может быть расположена или в плоскости верхней, или в плоскости нижней грани куба, вписанного в поверхность шара, если полагать плоскость Oxy расположенной горизонтально. Соответственно выбирается тот или иной знак во втором уравнении каждой из трёх систем.
Можно ли из этих систем уравнений получить уравнение траектории в виде одной формулы, я не знаю.
С уважением.
Как мне представляется, траектория состоит из трёх окружностей, оси которых попарно взаимно перпендикулярны. Выберем начало O декартовой прямоугольной системы координат в центре шара. Пусть первая окружность проецируется в натуральную величину на плоскость Oxy, вторая - на плоскость Oyz, третья - на плоскость Oxz.
Запишем уравнение поверхности шара:
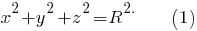
Первая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oxy на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.
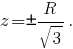
Вторая окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Oyz на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.
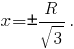
Третья окружность задаётся системой, состоящей из уравнения (1) и уравнения одной из плоскостей, расположенных от плоскости Ozx на расстоянии, равном половине стороны куба, вписанного в поверхность шара, т. е.
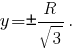
Каждая из окружностей, проецируясь одинаковым образом, может быть расположена в пространстве одним из двух способов. Например, первая окружность может быть расположена или в плоскости верхней, или в плоскости нижней грани куба, вписанного в поверхность шара, если полагать плоскость Oxy расположенной горизонтально. Соответственно выбирается тот или иной знак во втором уравнении каждой из трёх систем.
Можно ли из этих систем уравнений получить уравнение траектории в виде одной формулы, я не знаю.
С уважением.
Об авторе:
Facta loquuntur.
Facta loquuntur.
12.12.2015, 14:12
общий
Адресаты:
Вы уже потеряли интерес к этой задаче?
Об авторе:
Facta loquuntur.
Facta loquuntur.
12.12.2015, 18:11
общий
Уважаемый Андрей Владимирович,
Прошу извинить за задержку с ответом. Так как в постановочной части задачи подразумевался в том числе и отрицательный результат, а кроме заключения о невозможности получения уравнения траектории, получена величина отстояния плоскости окружности от центра шара (R/корень из трех), я считаю, что усилия были не напрасны и оцениваю Вашу работу на "хорошо". Благодарю Вас. Подумаю и попробую переформулировать задачу.
С наилучшими пожеланиями,
Георгий Шишков
Прошу извинить за задержку с ответом. Так как в постановочной части задачи подразумевался в том числе и отрицательный результат, а кроме заключения о невозможности получения уравнения траектории, получена величина отстояния плоскости окружности от центра шара (R/корень из трех), я считаю, что усилия были не напрасны и оцениваю Вашу работу на "хорошо". Благодарю Вас. Подумаю и попробую переформулировать задачу.
С наилучшими пожеланиями,
Георгий Шишков
12.12.2015, 20:37
общий
12.12.2015, 20:39
Адресаты:
Здравствуйте, Георгий!
Мы рады, что сотрудничество с Андреем Владировичем дало Вам импульс в исследовании задачи.
Только вот зачем было слать сообщение всем модераторам? Можно ж было адресовать только ему...
Ждем от Вас новых и интересных задач...
Мы рады, что сотрудничество с Андреем Владировичем дало Вам импульс в исследовании задачи.
Только вот зачем было слать сообщение всем модераторам? Можно ж было адресовать только ему...

Ждем от Вас новых и интересных задач...

Об авторе:
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
"Если вы заметили, что вы на стороне большинства, —
это верный признак того, что пора меняться." Марк Твен
Форма ответа
Отправка постов/ответов доступна только зарегистрированным и подтвержденным пользователям.
Если Вы уже зарегистрированы на Портале - войдите в систему, если Вы еще не регистрировались - пройдите простую процедуру регистрации.